Jakie są wewnętrzne alternatywne kąty? (Z ćwiczeniami)

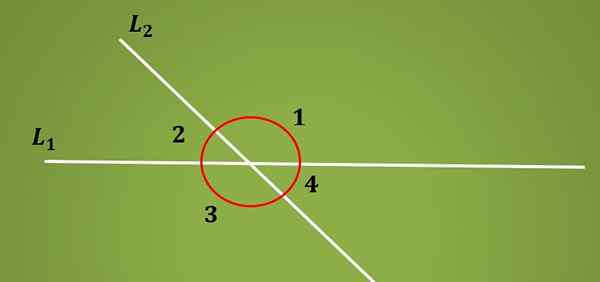
Wewnętrzne alternatywne kąty Są to kąty utworzone przez przecięcie dwóch równoległych linii i linii poprzecznej. Gdy linia L1 jest wycinana przez linię poprzeczną L2 4.

Dwie pary kąty, które pozostają po tej samej stronie linii L1, nazywane są kątami uzupełniającymi, ponieważ jej suma jest równa 180º. Na niższym obrazie kąt 1 i 2 są uzupełniające, a także kąty 3 i 4.

Aby porozmawiać o wewnętrznych alternatywnych kątach, konieczne jest posiadanie dwóch równoległych linii i linii poprzecznej; Jak widać wcześniej, powstanie osiem stron.

Gdy istnieją dwie równoległe linie L1 i L2 wycięte przez linię poprzeczną, powstaje osiem kątów, jak pokazano na następującym obrazie.

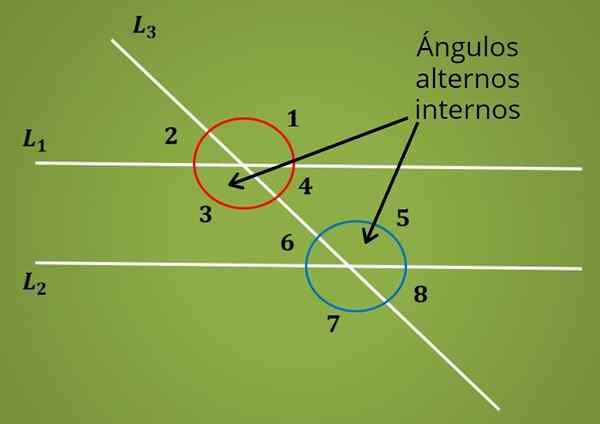
Na lepszym obrazie pary kąty 1 i 2, 3 i 4, 5 i 6, 7 i 8 są kątami uzupełniającymi. 

Teraz wewnętrzne alternatywne kąty znajdują się między dwiema równolegle L1 i L2, ale znajdują się po przeciwnych stronach linii poprzecznej L2. To jest Kąty 3 i 5 są wewnętrzne alternatywne. Podobnie kąty 4 i 6 są wewnętrznymi alternatywnymi kątami.

Przeciwne kąty przez wierzchołek

Aby poznać użyteczność, jaką mają wewnętrzne alternatywne kąty, najpierw konieczne jest wiedzieć, że jeśli dwa kąty są sprzeczne z wierzchołkiem, wówczas te dwa kąty mierzą to samo.

Na przykład kąty 1 i 3 mierzą to samo, co przeciwstawiają się wierzchołkowi. Zgodnie z tym samym uzasadnieniem można stwierdzić, że kąty 2 i 4, 5 i 7, 6 i 8 mierzą to samo.

Kąty utworzone między sekundą a dwoma podobieństwami

Gdy są dwie równoległe linie wycięte przez suchą lub poprzeczną linię, jak na poprzedniej figurze, prawdą jest, że kąty 1 i 5, 2 i 6, 3 i 7, 4 i 8 mierzą to samo.

Wewnętrzne alternatywne kąty

Korzystając z definicji kątów umieszczonych przez wierzchołek i właściwość kątów utworzonych między siedzącą a dwiema równolegle, można stwierdzić, że wewnętrzne alternatywne kąty mają tę samą miarę.

Rozwiązane ćwiczenia

- Pierwsze ćwiczenie

Oblicz miarę kąta 6 następującego obrazu, wiedząc, że kąt 1 mierzy 125º.

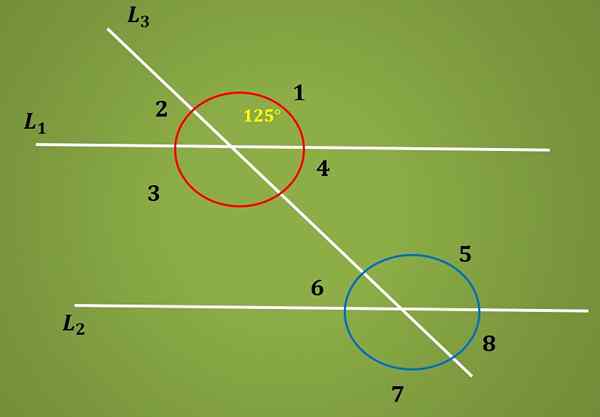
Rozwiązanie

Ponieważ kąty 1 i 5 są przeciwne przez wierzchołek, masz ten kąt 3 mierzy 125º. Teraz, ponieważ kąty 3 i 5 są wewnętrzne, masz ten kąt 5 również mierzy 125º.

Wreszcie, ponieważ kąty 5 i 6 są uzupełniające, miara kąta 6 jest równa 180º - 125º = 55º.

- Drugie ćwiczenie

Oblicz kąt 3, wiedząc, że kąt 6 mierzy 35º.

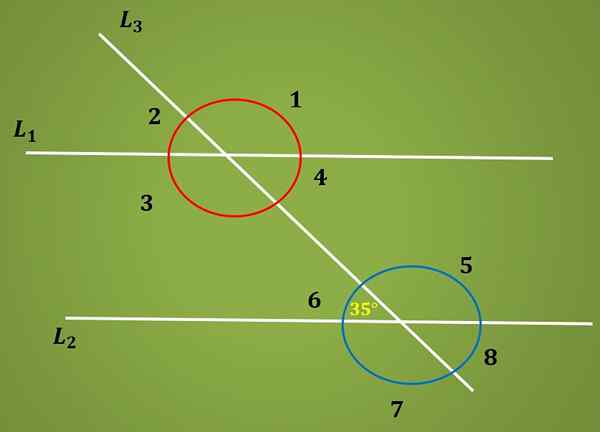
Rozwiązanie

Wiadomo, że kąt 6 mierzy 35º i wiadomo również, że kąty 6 i 4 są wewnętrzne, dlatego mierzą to samo. To znaczy, że kąt 4 mierzy 35º.

Z drugiej strony, stosując fakt, że kąty 4 i 3 są uzupełniające, miara kąta 3 jest równa 180º - 35º = 145º.

Obserwacja

Konieczne jest, aby linie były równoległe, aby mogły spełnić odpowiednie właściwości.

Ćwiczenia mogą zostać rozwiązane szybciej, ale ten artykuł chciał użyć własności wewnętrznych alternatywnych kątów.

Bibliografia

1. Bourke. (2007). Kąt w skoroszycie matematyki geometrii. Nauka Newpath.
2. Clemens, s. R., O'Dafer, s. 1. G., & Cooney, t. J. (1998). Geometria. Edukacja Pearsona.
3. Lang, s., & Murrow, G. (1988). Geometria: kurs szkoły średniej. Springer Science & Business Media.
4. Lira, a., Jaime, s. 1., Chavez, m., Gallegos, m., I Rodríguez, C. (2006). Geometria i trygonometria. Umbral Editions.
5. Moyano, a. R., Saro, a. R., & Ruiz, r. M. (2007). Algebra i geometria kwadratowa. Netbiblo.
6. Sullivan, m. (1997). Trygonometria i geometria analityczna. Edukacja Pearsona.
7. Wingard-Enelson, r. (2012). Geometria. Enslow Publishers, Inc.