Co reprezentuje długość przemieszczenia sześciokąta

Długość przemieszczenia sześciokąta reprezentuje Długość bocznych twarzy pryzmatu. Aby zrozumieć to stwierdzenie, pierwszą rzeczą, którą należy wiedzieć, jest to, że sześciokąt jest wielokątem składającym się z sześciu stron.

Może to być regularne, gdy wszystkie jego strony mają tę samą miarę; lub może być nieregularne, gdy przynajmniej jedna strona ma inną miarę od innych.

Najważniejsze, co należy zauważyć, że istnieje sześciokąt, a to musi zostać wyparte, to znaczy przeniesione z miejsca, wzdłuż linii, która przechodzi przez jego środek.

Teraz pytanie brzmi, co reprezentuje poprzednia długość przemieszczenia? Ważną obserwacją jest to, że wymiary sześciokąta nie mają znaczenia, tylko długość jego ruchu ma znaczenie.

Co reprezentuje przemieszczenie?

Przed odpowiedzią na pytanie tytułu warto wiedzieć, co reprezentuje przesunięcie z sześciokątem.

Oznacza to, że opiera się na założeniu, że istnieje regularny sześciokąt, a to jest przesunięte na pewną długość, wzdłuż linii, która przechodzi przez środek. Co generuje to przemieszczenie?

Jeśli zaobserwowano szczegółowo, można zauważyć, że powstaje heksagonalny pryzmat. Poniższa liczba lepiej ilustruje tę sprawę.

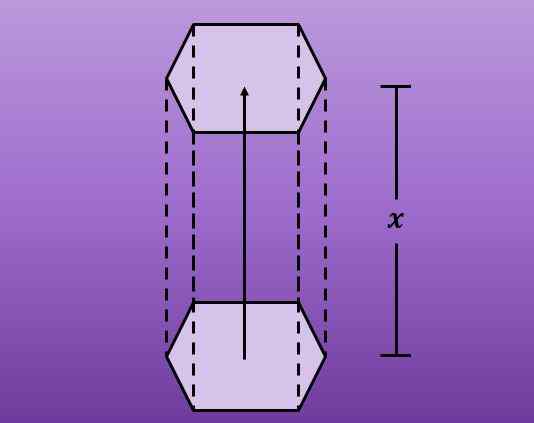
Co reprezentuje długość przesunięcia?

Według tego, co zostało powiedziane, przemieszczenie generuje heksagonalny pryzmat. I opisując poprzedni obraz, widać, że długość przemieszczenia sześciokąta reprezentuje długość bocznych twarzy pryzmatu.

Czy długość zależy od kierunku przesunięcia?

Odpowiedź brzmi nie. Przemieszczenie może mieć dowolny kąt nachylenia, a długość przesunięcia będzie nadal reprezentować długość bocznych twarzy utworzonego heksagonalnego pryzmatu.

Jeśli przemieszczenie odbywa się z kątem nachylenia między 0 ° a 90 °, powstanie ukośny heksagonalny pryzmat. Ale to nie zmienia interpretacji.

Poniższy obraz pokazuje figurę uzyskaną przez przesuwanie sześciokąta wzdłuż nachylonej linii, która przechodzi przez jej środek.

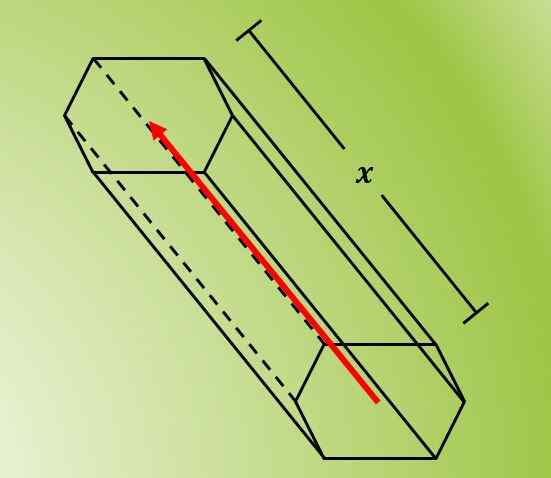
Ponownie, długość przemieszczenia jest długością bocznych twarzy pryzmatu.

Obserwacja

Kiedy przemieszczenie jest wykonywane wzdłuż linii prostopadłej do sześciokąt.

Innymi słowy, gdy powstaje prosty heksagonalny pryzmat, wówczas długość przemieszczenia jest wysokością pryzmatu.

Jeśli wręcz przeciwnie, linia ma inną nachylenie niż 90 °, wówczas długość przemieszczenia staje się hipotenusem trójkąta prostokąta, w którym kategoria wspomnianego trójkąta pokrywa się z wysokością pryzmatu pryzmatu.

Poniższy obraz pokazuje, co się dzieje, gdy sześciokąt wyświetla się po przekątnej.

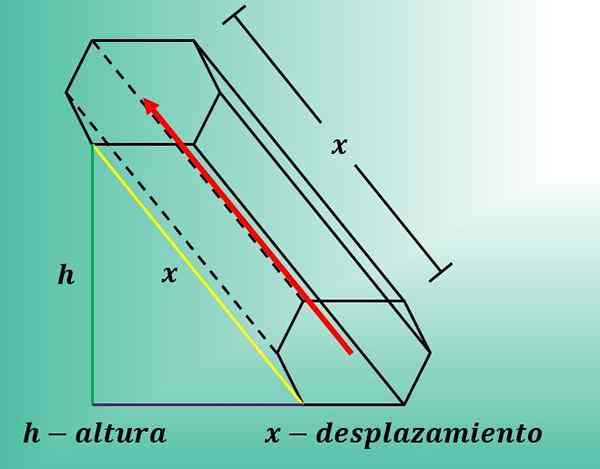
Wreszcie, ważne jest, aby podkreślić, że wymiary sześciokąta nie wpływają na długość przemieszczenia. 

Różni się, że można utworzyć prosty lub ukośny heksagonalny pryzmat.