Jakie są wytyczne? (Geometria)

dyrektywa W geometrii składa się z krzywej, powierzchni lub objętości, która pozostaje ustalona i określa sposób, w jaki tworzy się obiekt geometryczny. Na przykład według linii inne krzywe, takie jak stożkowe i rewolucyjne powierzchnie, takie jak prosty cylinder okrągły.

Krzywa wytycznych może być również obwodem. Prosty okrągły cylinder można utworzyć, pozostawiając promień Ri -r Rión Ri.

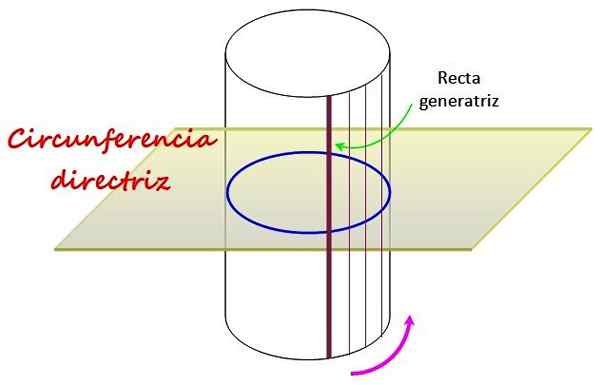
Rysunek 1. Prosty okrągły cylinder ma jako przewodnik, wokół którego porusza się linia o nazwie generatrix. Źródło: f. Zapata.

Obwód, który jest na płaszczyźnie narysowany na rysunku, określa kształt zakrzywionej powierzchni prostego cylindra okrągłego, który jest generowany przez obracanie linii wokół niej, zwanej zwaną Prosty generatrix.

Jeśli krzywa wskazówek nie jest obwodem, ale inną krzywą, generowane są inne typy cylindra, takie jak cylinder eliptyczny, którego wytyczną jest elipsa.

Obwód może również działać jako wytyczna w celu wygenerowania innej krzywej, taka jest przypadek Epitrokoid, Krzywa w płaszczyźnie generowanej przez punkt, który z kolei znajduje.

Łatwiej jest to docenić wizualnie przez następującą animację:

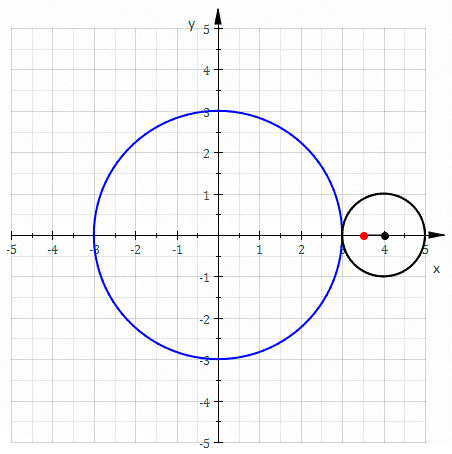Rysunek 2. Czerwona krzywa jest nazywana Epitrocid i jego wytyczne krzywa. Źródło: Wikimedia Commons. Sam Derbyshire w angielskiej Wikipedii/CC BY-S (http: // creativeCommons.Org/licencje/by-sa/3.0/).

Krzywa wytycznych na cylindrycznych powierzchniach

Cylindryczne powierzchnie są klasyfikowane zgodnie z ich krzywą wytyczną w cylindrach:

-Okólnik

-Eliptyczny

-Paraboliczny

-Hiperboliczny

Kiedy cylindryczna powierzchnia ma wytyczne, które leżą w płaszczyźnie prostopadłym do równania linii generatrix, równanie wspomnianej powierzchni jest takie same jak wytyczne wytycznych.

Może ci służyć: jaki jest związek między obszarem Rhombusa a prostokątem?

Cylindry należą do grupy Powierzchnie quadryczne, którego równanie to druga klasa z trzema zmiennymi. Ogólna forma to:

Topór² + Przez² + CZ² + DXY + EXZ + FYZ + GX + HY + IZ + K = 0

Gdzie współczynniki a, b, c ... to liczby rzeczywiste.

Cylindry są najczęstszymi i najczęstszymi trójwymiarowymi ciałami geometrycznymi, które można znaleźć, zwłaszcza proste cylindry okrągłe, ale inne typy cylindrów opisane poniżej również mają zastosowania w inżynierii i projektowaniu.

Prosty okrągły cylinder

Jego wytyczną jest koło C, które znajduje się w płaszczyźnie prostopadłym do cylindra, jak pokazano na rycinie 1, ponieważ linia generatrix, która biegnie do C, tworząc powierzchnię boczną, jest prostopadłe do C, jest prostopadłe do C.

Równanie obwodu C na płaszczyźnie XY, skupione na pochodzeniu (0,0) wynosi:

X² + I² = R²

Gdzie r, promień obwodu będzie oczywiście promieniem cylindra. Wysokość H cylindra rozciąga się wzdłuż osi Z, prostopadle do płaszczyzny XY.

Eliptyczny cylinder

Wytyczne to elipsa w płaszczyźnie XY wyśrodkowanej na pochodzeniu (0,0), którego równanie to:

Generatrix to linia prostopadła do płaszczyzny XY, która porusza się wokół elipsy, aby powstać na powierzchni bocznej. Elipsa może znajdować się na dowolnej wysokości Z na płaszczyźnie XY.

Na przykład elipsa równania:

4x² + 9Y² = 36

Jest to krzywa wytycznych, która powoduje powstanie cylindra eliptycznego, którego równanie to 4x² + 9Y² = 36, plus z = 0. Dodając to ostatnie wyrażenie, jasne jest, że jest to powierzchnia.

Może ci służyć: Błąd próbkowania: wzory i równania, obliczenia, przykłady

Cylinder paraboliczny

W takim przypadku wytyczna jest przypowieścią, która może mieć formę y = x². Zatem cylinder jest kierowany wzdłuż osi Z i tworzy układanie przypowieści z wierzchołkiem w (0,0) wzdłuż tej osi.

Cylinder paraboliczny ma zastosowanie w energii słonecznej, ponieważ niektórzy kolekcjonerzy mają w ten sposób lustra, przez które światło słoneczne jest skoncentrowane w skupieniu. Ten punkt przechodzi prostą rurę, w której olej osiąga temperatury do 400 ° C.

Cylinder hiperboliczny

W cylindrze hiperbolicznym równanie wytycznych jest hiperbola skoncentrowana na pochodzeniu:

Cylinder jest uformowany do stosu.

Powierzchnia rewolucji

Krzywa wytycznych powierzchni rewolucji jest ta sama oś rewolucji, wokół której krzywa odpowiedzialna za generowanie powierzchni.

Krzywa, która obraca się, może mieć dowolny kształt, w ten sposób obszar generowany jest jak widać w tej animacji:

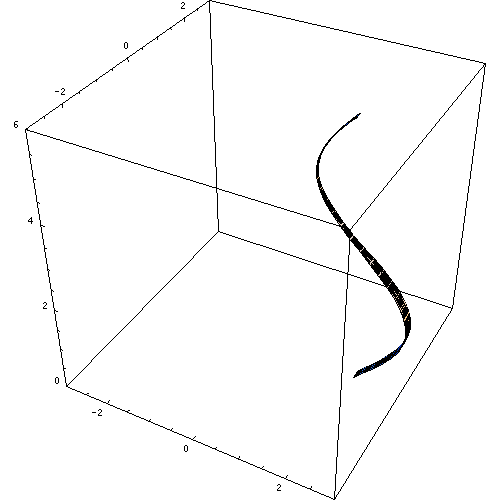Rysunek 3. Powierzchnia rewolucji. Źródło: Wikimedia Commons. https: // prześlij.Wikimedia.Org/wikipedia/commons/e/e7/rotationskoerper_animation.Gif.

Jeśli inna linia zostanie obrócona wokół wytycznych, otrzymano już znany prosty okrągły cylinder. W ten sam sposób można uzyskać inne powierzchnie rewolucji, takie jak stożkowe, sferyczne i toroidalne powierzchnie rewolucji.

Powierzchnia stożkowa

Stożowa powierzchnia jest generowana przez ruch linii generatrix, która zawsze przechodzi przez stałą krzywą płaską lub krzywą wytyczną oraz przez stały punkt zwany Vertex, który nie należy do płaszczyzny wytycznych.

Może ci służyć: matematyczna nadzieja: formuła, właściwości, przykłady, ćwiczenia

Wierzchołek lub końcówka dzieli stożek na dwie części, zwane liście albo gałęzie.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Znajdź boczny obszar wysokiego okrągłego cylindra o wysokości 25 cm, którego krzywą wytyczną jest obwód promienia 6 cm, skupiony na pochodzeniu.

Rozwiązanie

Boczny obszar cylindra jest iloczyn długości wytycznych według wysokości. Jeśli r jest promieniem obwodu, a H jest wysokością cylindra, obszar jest podany przez:

A = 2πr x h = 2πx 6 cm x 25 cm = 942.5 cm²

- Ćwiczenie 2

Masz następujące równanie, które odpowiada powierzchni quadrycznej:

X² + I² + 2Z² +2xz - 2yz = 1

Wskaż, jaka jest powierzchnia i jakie jest równanie wytycznych.

Rozwiązanie

Wykonanie z = k, gdzie k jest stałe, jest uzyskiwane:

X² + I² + 2K² +2KX - 2KY = 1

Zmieniamy warunki w następujący sposób:

(X² + 2kx) + (i²- 2KY) = 1-2K²

Kwadraty muszą², Aby nie zmieniać żadnego z nawiasów:

(X² + 2kx + k² - k² ) + (i² - 2KY + K² - k²) = 1-2K²

(X² + 2kx + k²) - k²  + (I²- 2KY + K²) - k² = 1-2K²

W ten sposób pozostaje:

(x + k)² + (i - k)² = 1

Podobnie jak równanie okręgu środkowego (-k, k) i promienia 1, powierzchnia jest prostym okrągłym cylindrem, również radia 1, o ile linia generatrix jest prostopadła do wspomnianego obwodu.

Na przykład, robiąc k = 0, równanie jest zmniejszone do obwodu wyśrodkowanego na pochodzeniu (0,0), którego promień wynosi 1:

X² + I² = 1

Bibliografia

1. Gaussianie. Reprezentują trzy -wymiarowe powierzchnie. Wyzdrowiały z: Gaussian.com.
2. Kindle, J. Teoria i problemy geometrii analitycznej. McGraw Hill. Seria Schaum.
3. Powierzchnie jako miejsca geometryczne. Odzyskany z: algebra.FRLP.Utn.Edu.ar.
4. Suárez, m. Powierzchnie. Źródło: tematy.UNQ.Edu.ar.
5. Powierzchnie quadryczne. Odzyskane z: systemów.fcincias.Unam.MX.