Pentagonalne charakterystyka pryzmatu, części, wierzchołki, krawędzie, objętość

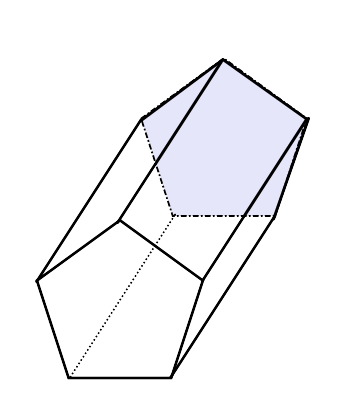
A Pentagonowy pryzmat Jest to trójwymiarowa postać geometryczna, której podstawy, identyczne, mają kształt pięciokąta, a także ma w sumie 5 -sesy w postaci równoległoboku.

Jeśli twarze są prostokątne, mówi się, że jest to Prosty pryzmat pięciokąta, Podczas gdy krawędzie są skłonne do podstaw, to jest to Skośny pryzmat pięciokąta. Na poniższym obrazie jest przykład każdego.

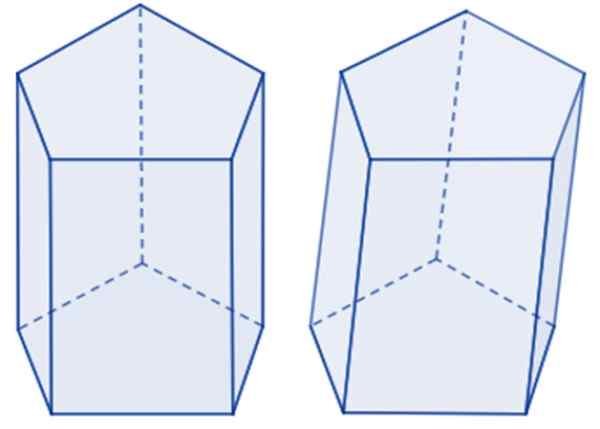Pięciokątny pryzmat po lewej i ukośnej po prawej stronie. Źródło: Wikimedia Commons.

Podstawowy Pentagon może być regularny, jeśli jego pięć stron ma tę samą miarę, a także kąty wewnętrzne, w przeciwnym razie jest to nieregularny Pentagon. Jeśli podstawa pryzmatu jest regularna, to jest o Regularny pryzmat pięciokąta. W przeciwnym razie jest pryzmat Nieregularny pięciokąta.

Nieregularne podstawowe pryzmaty Pentagonowe stosowane we współczesnej konstrukcji. Źródło: Flare tapety.

Pentagonowy pryzmat jest harmonijną strukturą stosowaną w architekturze i projektowaniu przedmiotów, takich jak nowoczesny budynek pokazany na górnej figurze. Nieregularne okna w kształcie Pentagonu tworzą podstawę pryzmatów.

[TOC]

Charakterystyka pryzmatu pięciokąta

-Jest to trójwymiarowa figura geometryczna, powierzchnie, które ją tworzą, zawierają określoną objętość.

-Ich podstawami są Pentagony, a ich boczne twarze mogą być prostokąty lub równoległoboki.

-Ma wierzchołki -narożniki prisma -i krawędzi -Bordy lub brzegi-.

-Jeśli krawędzie jednoczące podstawy są do nich prostopadłe, pryzmat jest prosty, a jeśli są nachylone, pryzmat jest ukośny.

-Kiedy podstawa jest pięciokątem, którego wewnętrzne kąty są mniejsze niż 180º, pryzmat jest wypukły, Ale jeśli jeden lub więcej kątów wewnętrznych jest większy niż 180º, jest to pryzmat wklęsły.

Pentagonalne elementy pryzmatu

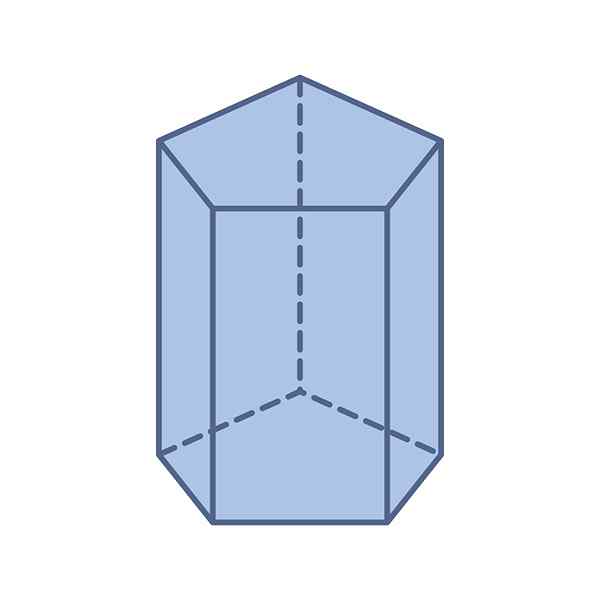
-Bazy: Ma dwie pięciokąta i przystające bazy -ich pomiary są takie same -albo regularne lub nieregularne.

Może ci służyć: ogólny wzór: równania kwadratowe, przykłady, ćwiczenia

-Twarze: Pentagonalny pryzmat ma w sumie 7 twarzy: dwie pięciokątny podstawy i pięć równoległoboków, które tworzą boki.

-Krawędź: segment, który łączy dwie podstawy, pokazane na czerwono na rycinie 3 lub ta, która łączy się z dwiema stronami.

-Wysokość: Odległość między twarzami. Jeśli pryzmat jest prosty, odległość ta zbiega się z rozmiarem krawędzi.

-Wierzchołek: Wspólny punkt między bazą i dwiema stronami bocznymi.

Dolna rysunek pokazuje regularny pryzmat pięciokątny, w którym segmenty tworzące podstawę mają taką samą miarę, zwaną Do.

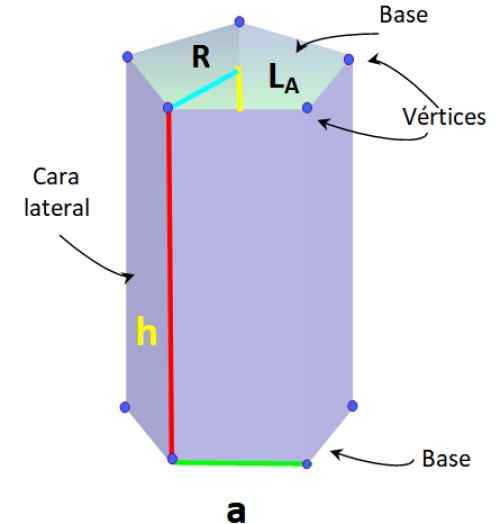 Regularne elementy pryzmatyczne pięciokąta. Źródło: f. Zapata.

Ten rodzaj pryzmatu ma również następujące elementy, typowe dla zwykłego Pentagonu:

-Radio r: Odległość między środkiem Pentagonu a jednym z wierzchołków.

-Apothem l_DO: segment, który dołącza do środka z punktem środkowym jednej z boków Pentagonu.

Ile wierzchołków ma pięciokątny pryzmat?

W Pentagonie istnieje 5 wierzchołków, a ponieważ pięciokątny pryzmat ma dwa pięciokrotnie jako podstawy, ciało to ma w sumie 10 wierzchołków.

Ile krawędzi ma pięciokątny pryzmat?

Możesz obliczyć liczbę krawędzi ciał geometrycznych z płaskimi twarzami, takimi jak pryzmaty, za pomocą Twierdzenie Euler Dla wypukłych wielościów. Leonhard Euler (1707-1783) jest jednym z największych matematyków i fizycznych w historii.

Twierdzenie określa związek między liczbą twarzy, którą nazwiemy C, ilością wierzchołków V i całkowitą krawędzi A w następujący sposób:

C+V = a+2

W przypadku pryzmatu pięciokąta: C = 7 i V = 10. Oczyszczanie, liczba krawędzi:

Może ci służyć: funkcja bijkłowców: co to jest, jak to się dzieje, przykłady, ćwiczenia

A = C+V-2

Wymiana wartości:

A = 7 + 10 - 2 = 15

Prism pięciokątny ma 15 krawędzi.

Jak uzyskać objętość pięciokątacznego pryzmatu?

Objętość pryzmatu pięciokątnego mierzy przestrzeń zablokowaną przez boki i podstawy. Jest to dodatnia kwota obliczana przez następującą właściwość:

Każda płaszczyzna, która przecina pryzmat prostopadle do jego krawędzi, generuje skrzyżowanie w taki sam sposób, jak podstawa, to znaczy pięciokąt o tych samych wymiarach.

Dlatego objętość pryzmatu pięciokątnego jest wynikiem obszaru podstawowego i wysokości pryzmatu.

Być DO_B Pentagonalny obszar bazowy i H Wysokość pryzmatu, a następnie objętość V Jest:

V = a_B x h

Ta formuła jest ogólna, jest ważna dla każdego pryzmatu, zwykłego lub nieregularnego, prostego lub skośnego.

Objętość pryzmatu zawsze pojawia się w jednostkach o wysokości długości na kostkę. Jeśli długość boków i wysokość pryzmatu podano w metrach, objętość wyraża się w m³, że „mierniki sześcienne” jest czytane. Inne jednostki to CM³, km³, cale³ i więcej.

- Regularna objętość pryzmatu pięciokąta

W Pentagonalnym pryzmatach regularne podstawy są regularnymi pięciokrotami, co oznacza, że ​​strony boczne i wewnętrzne są takie same. Biorąc pod uwagę symetrię ciała, obszar Pentagonu, a zatem objętość można łatwo obliczyć na kilka sposobów:

Znajomość wysokości i pomiaru boku

Być Do Miara pięciokątnej strony podstawowej. W takim przypadku obszar jest obliczany przez:

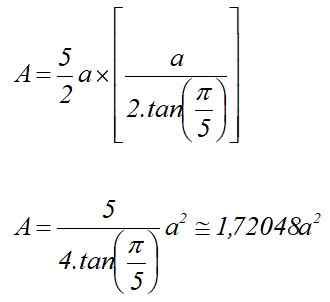
Dlatego objętość regularnego pięciokąta pryzmatu wysokości H wynosi:

Może ci służyć: wyobrażone liczby: właściwości, aplikacje, przykłady

V = 1.72048 a²⋅ h

Znajomość wzrostu i miary radia

Kiedy Radio r Z podstawy pięciokątnej to drugie równanie może być użyte w obszarze podstawowym:

A = (5/2) r²⋅ Sen 72º

W ten sposób objętość pięciokątnego pryzmatu jest podana przez:

V = (5/2) r² ⋅ H ⋅ Sen 72º

Gdzie H Jest to wysokość pryzmatu

Znajomość wysokości, miary wartości apotemii i obwodu

Pentagonalny obszar podstawowy można obliczyć, jeśli jego obwód P jest znany, co jest po prostu sumą boków, a także miarą apothem l l_DO:

A = p. L_DO / 2

Mnożenie tego wyrażenia przez wartość wysokości H, Mamy głośność pryzmatu:

V = P. L_DO .H / 2

- Nieregularna objętość pryzmatu pięciokąta

Wzór podany na początku jest nawet ważny, gdy podstawa pryzmatu jest nieregularnym pięciokąta:

V = a_B x h

Aby obliczyć obszar podstawowy, stosuje się różne metody, na przykład:

-Metoda triangulacji, która polega na podzieleniu Pentagonu na trójkąty i czworobok, których odpowiednie obszary można łatwo obliczyć. Obszar Pentagonu będzie sumą obszarów tych prostszych liczb.

-Metoda determinantów Gaussa, dla której musisz znać wierzchołki rysunku.

Po określeniu wartości obszaru mnoże się przez wysokość pryzmatu w celu uzyskania objętości.

Bibliografia

1. Alexander, zm. 2013. Geometria. 5. Wydanie. Cengage Learning.
2. Odniesienie do otwartego matematyki. Obszar wielokąta. Odzyskane z: Mathpenref.com.
3. Formuły wszechświata. Twierdzenie Eulera dla Polyhedros. Odzyskane z: Universoformulas.com.
4. Formuły wszechświata. Obszar zwykłego Pentagonu. Odzyskane z: Universoformulas.com.
5. Wikipedia. Pryzmat. Odzyskane z: jest.Wikipedia.com.
6. Wikipedia. Pentagonowy pryzmat. Odzyskane z: jest.Wikipedia.com.