Idealne liczby, jak je zidentyfikować i przykłady

A Idealna liczba to tak naturalna liczba Suma jego dzielników jest taka sama jak liczba. Oczywiście nie można go uwzględnić wśród dzielników do samej liczby.

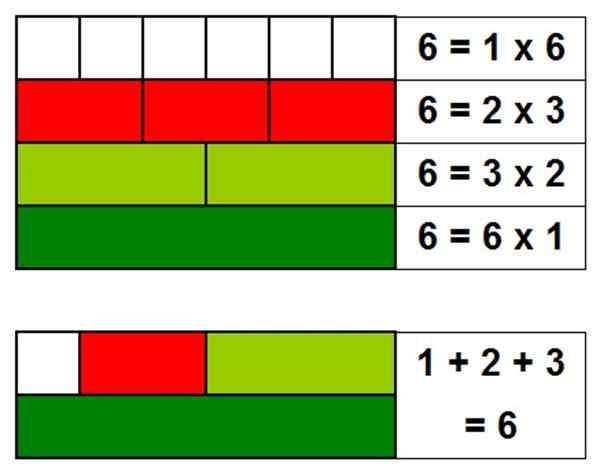
Jednym z najprostszych przykładów doskonałej liczby jest 6, ponieważ jego dzielnicy to: 1, 2 i 3. Jeśli dodamy dzielniki, otrzymujemy: 1 + 2 + 3 = 6.

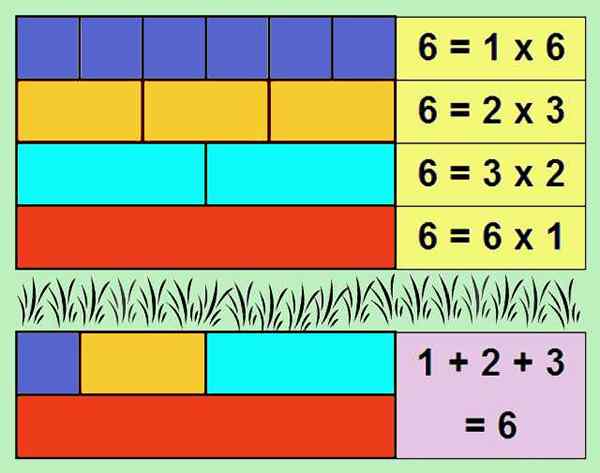Rysunek 1. Liczba 6 jest idealna, ponieważ suma jego dzielników, nie uwzględniając samej liczby, daje numer 6. Źródło: Self Made

Suma podziałów całkowitej, bez uwzględnienia samej liczby, jest nazywana podwielokrotność. Dlatego idealna liczba jest równa jej podwielokrotnie.

Ale jeśli w sumie dzielników liczby, liczba sama zostanie uwzględniona, wówczas liczba idealna będzie taka, że ​​suma wszystkich jego dzielników podzielonych przez 2 jest równa samej liczbie.

[TOC]

Historia

Matematycy starożytności, zwłaszcza Greków, przyznali ogromne liczby i przypisywane boskie cechy.

Na przykład Philo de Alejandría, około I wieku, twierdził, że 6 i 28 to doskonałe liczby, które pokrywają się z sześcioma dniami stworzenia świata i dwudziestu osiem.

Idealne liczby są również obecne w naturze, na przykład na północnym biegunie Saturn, pojawia się również idealna liczba 6, wiru w kształcie sześciokątnym znalezione przez sondę Cassini, która zaintrygowała naukowcom. 

Pszczoły plastyczne plastra miodu mają komórki w postaci sześciokątnej, to znaczy z 6 stronami.  Pokazano, że wielokąt o idealnej liczbie 6 jest tym, który umożliwia maksymalizację liczby komórek w ulu pszczół, z minimalnym woskiem do jego opracowania.

Rysunek 2. Idealny numer 6 jest obecny w pszczoły plaster miodu. Pokazano, że z tą liczbą boków ilość wosku, która ma być użyta do utworzenia komórek, jest minimalna. Źródło: Pixabay.

Idealne właściwości liczb

Suma wszystkich dzielników liczby naturalnej n jest oznaczona przez σ (n). W doskonałej liczbie prawdą jest, że: σ (n) = 2n.

Formuła i kryteria euklida

Euclid odkrył formułę i kryterium, które pozwalają znaleźć idealne liczby. Ta formuła to:

2^(N-1) (2^N -1)

Jednak liczba wygenerowana przez formułę będzie idealna tylko wtedy, gdy czynnik (2^N -1) Bądź kuzynem.

Może ci służyć: prostokątne elementy wektora (z ćwiczeniami)

Zobaczmy, jak generowane są pierwsze idealne liczby:

Jeśli n = 2, to mamy 2¹ (2² - 1) = 2 x 3 = 6, które już widzieliśmy, że jest idealny.

Kiedy n = 3 masz 2² (2³ - 1) = 4 x 7 = 28, co jest również idealne, ponieważ jest szczegółowo weryfikowane w przykładzie 1.

Zobaczmy, co się stanie z n = 4. Zastępując formułę Euclida:

2³ (2⁴ - 1) = 8 x 15 = 120

Można zweryfikować, że liczba ta nie jest idealna, jak pokazano szczegółowo w przykładzie 3. Nie jest to sprzeczne z kryteriami Euclida, ponieważ 15 nie jest kuzynem, niezbędnym wymogiem, aby wynik był doskonałą liczbą.

Zobaczmy, co się stanie, gdy n = 5. Stosując formułę, którą mamy:

2⁴ (2⁵ - 1) = 16 x 31 = 496

Ponieważ 31 jest liczbą pierwszą, więc numer 496 musi być doskonały, zgodnie z kryteriami Euclida. W przykładzie 4 szczegółowo pokazano, że jest skutecznie.

Liczby podstawowe, które mają formularz 2^P - 1 nazywają się kuzynami Mersenne, na cześć mnicha Marina Mersenne'a, który studiował liczby główne i doskonałe liczby w XVII wieku.

Następnie w XVIII wieku Leonhard Euler pokazał, że cała idealna liczba generowana przez formułę Euclida to pary.

Do tej pory znaleziono idealne miejsce, które jest dziwne.

Największy doskonały numer

Do bieżącej daty znanych jest 51 doskonałych liczb, wszystkie generowane przez formułę i kryteria euclida. Liczba ta uzyskano po znalezieniu kuzyna Mersenne'a, czyli: (2^82589933 - 1).

Idealna liczba #51 to (2^82589933) X (2^82589933 - 1) i ma 49724095 digitos.

Idealna liczba jest przyjacielem siebie

W teorii liczb mówi się, że dwie liczby są przyjaciółmi, gdy suma dzielników jednego, nie uwzględniając samej liczby, jest równa drugiej liczbie i odwrotnie.

Może ci służyć: segment linii i półiany

Czytelnik może sprawdzić, czy suma dzielników 220, bez uwzględnienia 220 wynosi 284. Z drugiej strony suma dzielników 284, nie uwzględniająca 284, wynosi 220. Dlatego liczby par 220 i 284 są przyjaciółmi.

Z tego punktu widzenia idealna liczba jest swoim przyjacielem.

Przykłady doskonałych liczb

Następnie wymieniono pierwsze osiem idealnych liczb:

6

28

496

8128

33550336

8589869056

137438691328

2305843008139952128

Ćwiczenia

W następujących ćwiczeniach konieczne będzie obliczenie dzielników liczby, a następnie wykonanie ich suma i sprawdzenie, czy liczba jest liczbą idealną, czy nie.

Dlatego przed zajęciem się ćwiczeniami przeglądamy koncepcję i pokażemy, w jaki sposób są one obliczane.

Na początek musisz pamiętać, że liczbą mogą być kuzynami (gdy można je podzielić tylko na siebie i 1) lub związki (gdy mogą się rozłożyć jako produkt liczb pierwszych).

Dla liczby złożonej n masz:

N = a^N . B^M. C^P … R^k 

Gdzie a, b, c ... r to liczby pierwszymi i n, m, p ... k są wykładnikami należącymi do liczb naturalnych, co może być warte od 1 od 1.

Jeśli chodzi o te wykładniki, istnieje formuła, aby wiedzieć, ile dzielników ma liczba n, chociaż nie mówi nam, co to jest. Niech C będzie taką kwotą, zatem:

C = (n +1) (m +1) (p +1) ... (k +1)

Rozkład liczby N jako produktu liczb pierwszych i wiedza o tym, ile ma dzielników, zarówno kuzynów, jak i nie -okoizynów, pomoże nam ustalić, jakie są ci dzielnicy.

Gdy wszyscy mają, z wyjątkiem ostatniej, która nie jest wymagana w sumie, można go zweryfikować, czy jest to idealna liczba, czy nie.

- Ćwiczenie 1

Sprawdź, czy numer 28 jest idealny.

Rozwiązanie

Pierwszym z nich będzie rozkładanie liczby w jego głównych czynnikach.

28 | 2
14 | 2
07 | 7
01 | 1

Jego dzielnicy to: 1, 2, 4, 7, 14 i 28. Jeśli wykluczymy 28, suma dzielników daje:

Może ci służyć: połowa 15

1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28

Dlatego 28 jest idealną liczbą.

Ponadto suma wszystkich jego dzielników wynosi 28 + 28, więc reguła σ (28) = 2 x 28.

- Ćwiczenie 2

Zdecyduj, czy numer 38 jest idealny, czy nie.

Rozwiązanie

Liczba jest podzielona na jej główne czynniki:

39 | 3
13 | 13
01 | 1

Divisorzy 39 bez włączenia liczby to: 1, 3 i 13. Suma 1 + 3 + 13 = 4 + 13 = 17 nie jest równa 39, dlatego 39 jest niedoskonałą lub nieopuszczalną liczbą. 

- Ćwiczenie 3

Dowiedz się, czy numer 120 jest doskonały czy niedoskonały.

Rozwiązanie

Liczba jest podzielona na jej główne czynniki:

120 | 2
060 | 2
 30 | 2
 15 | 3
  5 | 5
  1 | 1

Z podstawowych czynników znaleziono dzielniki:

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 i 120

Gdyby 120 było idealne przy dodaniu wszystkich jego dzielników, należy uzyskać 2 x 120 = 240. 

1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360

Ten wynik wyraźnie różni się od 240, więc stwierdzono, że numer 120 nie jest idealną liczbą.

- Ćwiczenie 4

Sprawdź, czy liczba 496, uzyskana według kryteriów Euclida, jest idealną liczbą.

Rozwiązanie

Liczba 496 jest podzielona na jego główne czynniki:

496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1

Wtedy ich dzielnicy to:

1, 2, 4, 8, 16, 31, 62, 124, 248, 496

Teraz wszystkie są dodawane, z wyjątkiem 496:

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Potwierdzanie, że jest to rzeczywiście idealna liczba.

Bibliografia

1. Baldor, a. 1986. Arytmetyka. Codex Editions and Dystrybucje.
2. Wszystko o liczbach pierwotnych. Liczby przyjaciół. Odzyskane od: pielęgniarka.org.
3. Wolfram Mathworld. Reguła Eulera. Odzyskane z: Mathworld.Wolfram.com.
4. Wolfram Mathworld. Idealna liczba. Odzyskane z: Mathworld.Wolfram.com.
5. Wikipedia. Idealne liczby. Źródło: w:.Wikipedia.org.
6. Wikipedia. Liczby przyjaciół. Odzyskane z: jest.Wikipedia.org.