Moment formuł bezwładności, równania i przykłady obliczeń

On moment bezwładności Z sztywnego ciała w odniesieniu do pewnej osi obrotu, reprezentuje jego odporność na zmianę prędkości kątowej wokół tej osi. Jest proporcjonalny do masy, a także do lokalizacji osi obrotu, ponieważ ciało, zgodnie z jego geometrią, może łatwiej obracać się wokół niektórych osi niż u innych.

Załóżmy, że rozległy obiekt (składający się z wielu cząstek), który może obracać się wokół osi. Załóżmy, że siła działa F, stycznie zastosowane do elementu masy Δm_Siema, To wytwarza moment obrotowy lub moment, który podano τ_internet = ∑R_Siema X F_Siema. Wektor R_Siema Jest to pozycja Δm_Siema (Patrz Rysunek 2).

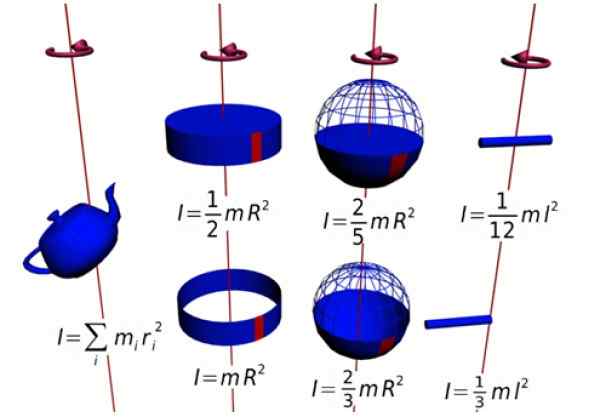
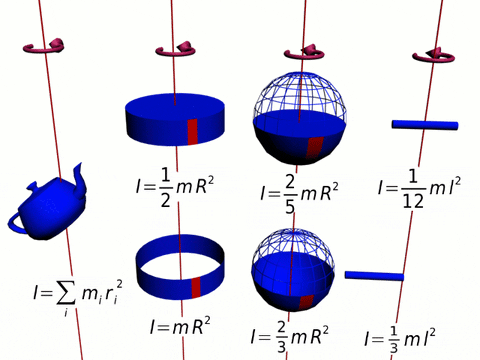Rysunek 1. Chwile bezwładności kilku postaci. Źródło: Wikimedia Commons.

Ten moment jest prostopadły do ​​płaszczyzny obrotowej (adres +K = opuszczanie papieru). Ponieważ wytrzymałość i pozycja promieniowa są zawsze prostopadłe, produkt krzyżowy pozostaje:

τ_internet = ∑ f_Siema R_Siema k = ∑ (δm_Siema Do_Siema) R_Siema  k = ∑ δm_Siema (Do_Siema R_Siema ) k

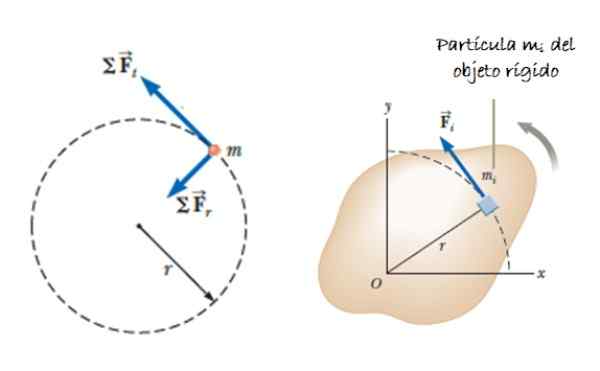Rysunek 2. Cząstka należąca do sztywnej substancji stałej w rotacji. Źródło: Serway, r. 2018. Fizyka nauk i inżynierii. Tom 1. Cengage Learning.

Przyspieszenie a_Siema reprezentuje styczny składnik przyspieszenia, ponieważ przyspieszenie promieniowe nie przyczynia się do momentu obrotowego. W zależności od przyspieszenia kątowego α możemy wskazać, że:

Do_Siema = α r_Siema

Dlatego moment obrotowy netto jest taki:

τ_internet = ∑ δm_Siema (α r_Siema²) K = (∑ R_Siema² Δm_Siema) α k

Przyspieszenie kątowe α jest takie samo dla całego obiektu, dlatego nie ma wpływu na indeks dolnej „I” i może pozostawić sumę, która jest dokładnie momentem bezwładności symbolizowanego obiektu z literą I:

I = ∑ r_Siema² Δm_Siema

To jest moment bezwładności dyskretnego rozkładu masy. Gdy rozkład jest ciągły, suma jest zastąpiona całką i Δm staje się masową różnicą DM. Integral jest wykonywany przede wszystkim obiektem:

I = ∫_M(R²) DM

Jednostki momentu bezwładności w systemie międzynarodowym, jeśli są one kg x m². Jest to skalar i ilość dodatnia, ponieważ jest produktem ciasta przy kwadratowi odległości.

[TOC]

Przykłady obliczeń

Rozszerzony obiekt, taki jak pasek, dysk, kula lub inny, którego gęstość ρ Jest to stałe i wiedząc, że gęstość jest ilorazem masy - objętości, różnica masy DM Jest napisane jako:

ρ = DM/DV → DM = ρDV

Zastępując całkę na chwilę bezwładności, mamy:

I = ∫r² ρdv = ρ ∫r²DV

Jest to ogólne wyrażenie, ważne dla obiektu trójwymiarowego, którego objętość V i pozycja R Są funkcjami współrzędnych przestrzeni X, I I z. Zauważ, że będąc stałym, gęstość jest poza całką.

Gęstość ρ Jest również znany jako gęstość objętościowa, ale jeśli obiekt jest bardzo płaski, jako arkusz lub bardzo cienki i wąski jak pręt, można użyć innych form gęstości, zobaczmy:

Może ci służyć: ruch rotacji Ziemi

- Dla bardzo drobnego arkusza gęstość do użycia wynosi σ, gęstość powierzchniowa (masa na jednostkę) i daje to różnica obszaru.

- A jeśli jest to cienki pręt, w którym istotna jest tylko długość, stosuje się gęstość masy liniowej λ i różnica długości, zgodnie z osą używaną jako odniesienie.

W poniższych przykładach wszystkie obiekty są uważane za sztywne (nieformalne) i mają jednolitą gęstość.

Moment bezwładności cienkiego paska w odniesieniu do osi, która przechodzi przez jej środek

Tutaj obliczymy moment bezwładności cienkiego, sztywnego, jednorodnego pręta o długości L i Mass M, w odniesieniu do osi, która przechodzi za pomocą środków.

Po pierwsze, konieczne jest ustanowienie systemu współrzędnych i zbudowanie liczby o odpowiedniej geometrii, takiej jak ten:

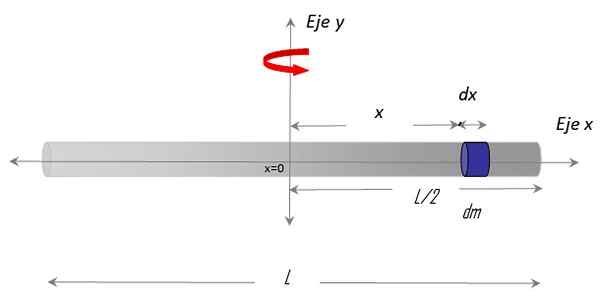Rysunek 3. Geometria do obliczenia momentu bezwładności cienkiej pręta w odniesieniu do osi pionowej, która przechodzi przez jej środek. Źródło: f. Zapata.

Został wybrany Oś x wzdłuż baru i Oś y jako oś obrotu. Procedura ustanowienia całki wymaga również wyboru masy różnicowej na pasku, nazywanym DM, który ma różnicową długość Dx i znajduje się w pozycji X arbitralne, w odniesieniu do centrum x = 0.

Zgodnie z definicją liniowej gęstości masy λ:

λ = m/l

Gdy gęstość jest jednolita, co jest ważne dla M i L, dotyczy również DM i DX:

λ = DM/DX → DM = λDX.

Z drugiej strony element masy jest w pozycji X, Następnie zastępując tę ​​geometrię w definicji, mamy określoną całkę, której granice są skrajności paska zgodnie z układem współrzędnych:

Zastąpienie gęstości liniowej λ = m/l:

Aby znaleźć moment bezwładności paska w odniesieniu do innej osi obrotu, na przykład ta, która przechodzi przez jeden z jego końca, możesz użyć twierdzenia Steiner (patrz ćwiczenie rozwiązane na końcu) lub wykonać bezpośrednie obliczenia podobne do tego pokazane tutaj, ale prawidłowo modyfikująca geometrię.

Moment bezwładności albumu w odniesieniu do osi, która przechodzi przez jego centrum

Bardzo cienki album z nikczemną grubością to płaska postać. Jeśli ciasto jest równomiernie rozmieszczone w całym obszarze A, gęstość masy σ to:

σ = M/a

Aż tak bardzo DM Jak daje odpowiadają masie i obszarowi różnicowego pierścienia pokazanego na rysunku. Zakładamy, że cały zestaw obraca się wokół osi i.

Możesz sobie wyobrazić, że album jest komponowany, że wiele radio koncentrycznych pierścieni R, każdy z odpowiednim momentem bezwładności. Dodając wkład wszystkich pierścieni, dopóki nie dotrzesz do radia R, Będziesz miał całkowitą bezwładność albumu.

σ = DM/DA → DM = σdaje

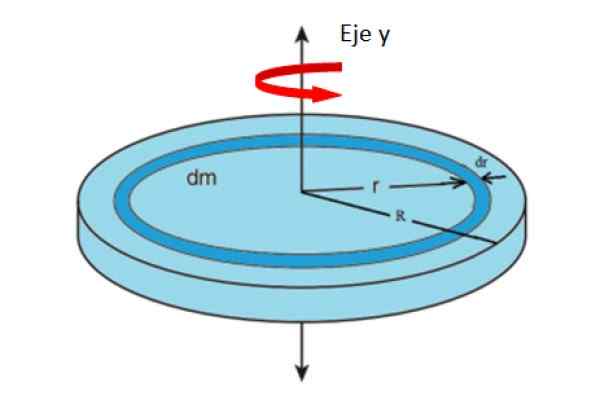Rysunek 4. Geometria do obliczenia momentu bezwładności albumu, w odniesieniu do osi osiowej. Źródło: f. Zapata.

Gdzie M reprezentuje całe ciasto albumu. Obszar albumu zależy od jego promienia r jako:

Może ci służyć: prędkość propagacji fali

A = π.R²

Duszowanie o R:

DA /DR = 2 = 2π.R → Da = 2π.RDR

Zastąpienie powyższego w definicji I:

Po ocenie integralnych wyników:

Zastąpienie σ = m/(π.R² ) pozostaje:

Moment bezwładności stałej kuli w odniesieniu do średnicy

Sfera promieniowa można uznać za serię układanych płyt na sobie, gdzie każdy nieskończenie masowy album DM, radio R i grubość Dz, Ma chwilę bezwładności::

dał_dysk = (½) r²DM

Aby znaleźć tę różnicę, formuła poprzedniej sekcji została po prostu wzięta i wymieniona M I R przez DM I R, odpowiednio. Taki album można zobaczyć w geometrii ryc. 5.

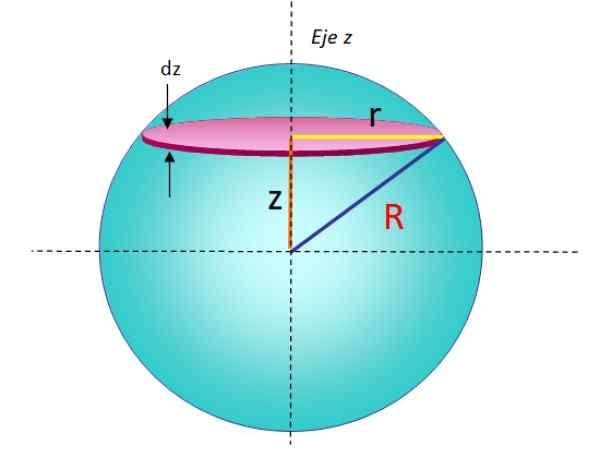Rysunek 5. Geometria do obliczenia momentu bezwładności kuli promienia stałego w odniesieniu do osi, która przechodzi przez średnicę. Źródło: f. Zapata.

Dodając wszystkie momenty nieskończenie małej bezwładności układów ułożonych, moment całkowitej bezwładności kuli:

Siema_kula = ∫di_dysk

Co jest równoważne:

I = ∫_kula (½) r²DM

Aby rozwiązać całkę, musisz wyrazić DM odpowiednio. Jak zawsze osiąga się to z gęstości:

ρ = m/v = dm/dv → dm = ρ.DV

Objętość różnicowego dysku to:

DV = powierzchnia podstawy x wysokość

Wysokość albumu to grubość Dz, Podczas gdy obszar podstawowy jest πr², W związku z tym:

Dv = πr²Dz

A zastąpienie w zintegrowanym byłoby takie:

I = ∫_kula(½) r²DM = ∫ (½) r²(ρπr²Dz)

Ale przed zintegrowaniem musi to. Przez twierdzenie Pitagorasa:

R² = r² + z² → R² = R² - z²

 To prowadzi nas do:

I = ∫_kula(½) ρ r²(πr²dz) = ∫_kula(½) ρ π r⁴Dz= ∫_kula(½) ρ π (r² - z²)² Dz

Aby zintegrować całą kulę, zauważamy, że Z zmienia się między -r i r, dlatego:

Wiedząc to ρ = m/v = m/[(4/3) πr³] Na koniec jest uzyskiwane po uproszczeniu:

Moment bezwładności cylindra stałego w odniesieniu do osi osiowej

W przypadku tego obiektu stosuje się metodę podobną do tego zastosowanego dla kuli, tylko tym razem jest łatwiejsze, jeśli cylinder jest wyobrażony dla radiowych powłok cylindrycznych R, grubość Dr i wysokość H, Jakby były warstwami cebuli.

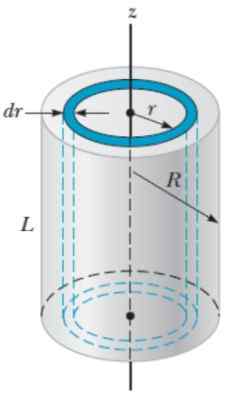Rysunek 6. Geometria do obliczenia momentu bezwładności cylindra promienia stałego R. Źródło: Serway, r. 2018. Fizyka nauk i inżynierii. Tom 1. Cengage.

Objętość DV warstwy cylindrycznej to:

DV = 2π.Rl.Dr

Dlatego masa kasyna to:

Może ci służyć: Skala mikroskopowa: właściwości, cząstki zliczania, przykłady

DM = ρ.Dv = ρ. 2π.R.L.Dr

To wyrażenie zastępuje się w definicji momentu bezwładności:

 Jeśli się uwzględni ρ = m / (π.R²L) zostaje:

Poprzednie równanie wskazuje, że moment bezwładności cylindra nie zależy od jego długości, ale tylko od jego masy i promienia. Tak L Zmieniono moment bezwładności w odniesieniu do osi osiowej. Z tego powodu, Siema cylindra zbiega się z wcześniej obliczonym cienkim albumem.

Moment bezwładności prostokątnego arkusza w odniesieniu do osi, która przechodzi przez jej środek

Oś y Pozioma jako oś obrotu. Poniższy rysunek pokazuje niezbędną geometrię do wykonania integracji:

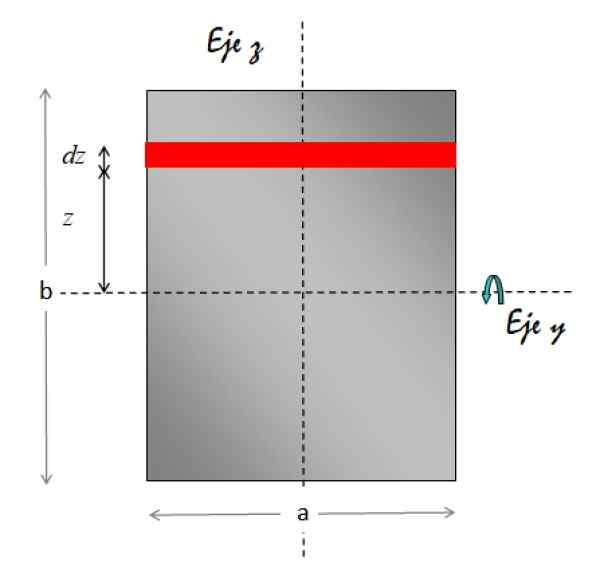Rysunek 7. Geometria do obliczania momentu bezwładności prostokątnej płyty w odniesieniu do osi równoległej do arkusza, która przechodzi przez jej środek. Źródło: f. Zapata.

Element obszaru wskazany na czerwono jest prostokątny. Jego powierzchnia to wysokość podstawy X, zatem:

DA = a.Dz

Dlatego masowa różnica wynosi:

DM = σ.DA = σ.(Do.Dz)

Jeśli chodzi o odległość elementu powierzchni od osi obrotu, zawsze jest z. Wymieniamy to wszystko w całce momentu bezwładności:

Teraz gęstość masy powierzchniowej σ jest zastępowana przez:

σ = m/ab

I to jest zdecydowanie takie:

Zauważ, że jest to jak cienki pasek.

Moment bezwładności kwadratowej arkusza w odniesieniu do osi, która przechodzi przez jej środek

Na kwadrat z boku L, W poprzednim wyrażeniu ważnym dla prostokąta, wartość B przez jeden L:

Twierdzenia momentu bezwładności

Istnieją dwa szczególnie przydatne twierdzenia, aby uprościć obliczenie momentów bezwładności w odniesieniu do innych osi, które w przeciwnym razie można było znaleźć z powodu braku symetrii. Te twierdzenia to:

Twierdzenie Steinera

Nazywane również Twierdzenie o osi równoległej, odnosi moment bezwładności dotyczącej osi z inną, która przechodzi przez środek masy obiektu, o ile osie są równoległe. Aby go zastosować, odległość D musi być znana między dwiema osiami i oczywiście masą M obiektu.

Być Siema_z moment bezwładności rozszerzonego obiektu w odniesieniu do Z, i oś_Cm Moment bezwładności w odniesieniu do osi, która przechodzi przez centrum masy (cm) wspomnianego obiektu, wówczas spełnia się, że:

Siema_z = I_Cm + MD²

Lub w notacji z poniższego rysunku: Siema_{z '} = I_z + MD²

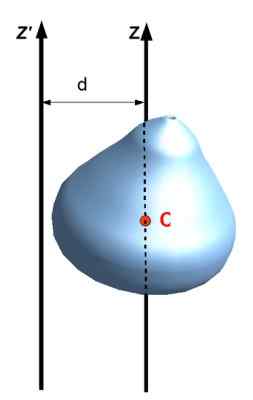Cyfra 8. Twierdzenie Steinera lub osie równoległe. Źródło: Wikimedia Commons. Jack patrz [CC BY-SA (https: // creativeCommons.Org/licencje/by-sa/3.0)]

Twierdzenie o osi prostopadłej

Twierdzenie to dotyczy płaskich powierzchni i mówi: moment bezwładności płaskiego obiektu wokół osi prostopadłej do niej jest sumą momentów bezwładności wokół dwóch osi prostopadłowych do pierwszej osi:

Siema_z = I_X + Siema_I

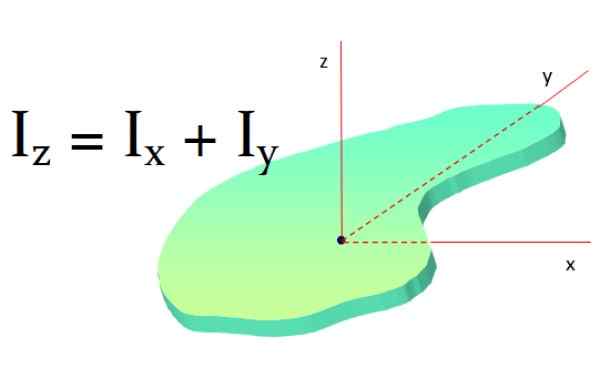Rysunek 9. Twierdzenie o osi prostopadłej. Źródło: f. Zapata.

Jeśli obiekt ma taką symetrię Siema_X I Siema_I Są takie same, wtedy spełnia się, że:

Siema_z = 2i_X

Ćwiczenie rozwiązane

Znajdź moment bezwładności paska w odniesieniu do osi, która przechodzi przez jeden z jego końca, na przykład ten pokazany na rycinie 1 (poniżej i po prawej) i ryc. 10.

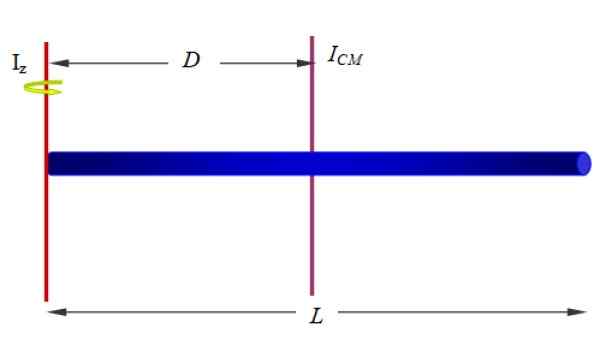Rysunek 10. Moment bezwładności jednorodnego baru wokół osi, który przechodzi przez jeden koniec. Źródło: f. Zapata.

Rozwiązanie:

Mamy już moment bezwładności paska wokół osi, która przechodzi przez jego geometryczne centrum. Ponieważ bar jest jednorodny, jego środek masy jest w tym momencie, więc będzie to nasze Siema_Cm Zastosować twierdzenie Steinera.

Jeśli długość paska jest L, Oś Z jest w odległości d = l/2, dlatego:

Siema_z = I_Cm + MD²= (1/12) ml²+M (l/2)²= (1/3) ml²

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill. 313-340
2. Rex, a. 2011. Podstawy fizyki. osoba. 190-200.
3. Twierdzenie o osi równoległej. Odzyskane z: Hiperphysics.Phy-orst.GSU.Edu.
4. Serway, r. 2018. Fizyka nauk i inżynierii. Tom 1. Cengage.
5. Uniwersytet Sevilla. Moment bezwładności sferycznych stałych. Odzyskany z: Laplace.nas.Jest.
6. Uniwersytet Sevilla. Moment bezwładności układu cząstek. Odzyskany z: Laplace.nas.Jest.
7. Wikipedia. Twierdzenie o osi równoległej. Źródło: w:.Wikipedia.org