Odwrotne obliczenia macierzy i ćwiczenia rozwiązane

Odwrotna macierz danej matrycy, jest to macierz pomnożona przez oryginalne wyniki w macierzy tożsamości. Matryca odwrotna jest przydatna do rozwiązywania układów równań liniowych, stąd znaczenie wiedzy, jak ją obliczyć.

Matryce są bardzo przydatne w fizyce, inżynierii i matematyce, ponieważ są kompaktowym narzędziem do rozwiązywania złożonych problemów. Użyteczność macierzy jest wzmocniona, gdy są one odwrócone, a ich odwrotność jest znana.

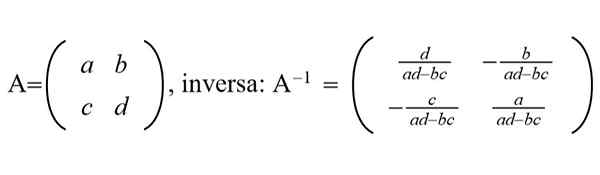Rysunek 1. Pokazano ogólną matrycę 2 × 2 i jej odwrotną matrycę. (Przygotowane przez Ricardo Pérez)

W polach przetwarzania graficznego duże zbiory danych, eksploracja danych, uczenie maszynowe i inne są wykorzystywane wydajne i szybkie algorytmy do oceny macierzy odwrotnej macierzy NXN z n bardzo dużą, w kolejności tysięcy lub milionów.

Aby zilustrować zastosowanie macierzy odwrotnej w zarządzaniu systemem równań liniowych, zaczniemy od najprostszego przypadku: 1 × 1 macierzy.

Najprostszy przypadek: uwzględniono równanie liniowe pojedynczej zmiennej: 2 x = 10.

Chodzi o to, aby znaleźć wartość x, ale będzie to „Matrixly”. 

Matryca m = (2), która mnoży wektor (x), jest macierzą 1 × 1, która powoduje wektor (10):

M (x) = (10)

Odwrotność matrycy M jest oznaczona przez M^-1.

Ogólnym sposobem pisania tego „systemu liniowego” jest:

M x = b, gdzie x jest wektorem (x), a B jest wektorem (10).

Z definicji macierz odwrotnej to taka, która pomnożona przez oryginalną macierz powoduje macierz tożsamości I:

M^-1 M = i

W rozważanym przypadku matryca M^-1 To macierz (½), czyli m^-1 = (½) od m^-1 M = (½) (2) = (1) = i

Może ci służyć: 90 dzielników: co to jest i wyjaśnienie

Aby znaleźć nieznany wektor x = (x), w podniesionym równaniu obaj członkowie są mnożone przez macierz odwrotnej:

M^-1 M (x) = m^-1 (10)

(½) (2) (x) = (½) (10)

(½ 2) (x) = (½ 10)

(1) (x) = (5)

(x) = (5)

Osiągnięto równość dwóch wektorów, które są takie same tylko wtedy, gdy ich odpowiednie elementy są równe, czyli x = 5.

Obliczanie odwrotności matrycy

Motywuje obliczenie macierzy odwrotnej, jest znalezienie uniwersalnej metody rozwiązania układów liniowych, takich jak następujący system 2 × 2:

x - 2 y = 3

-x + y = -2

Podążając za etapami przypadku 1 × 1, badanym w poprzedniej sekcji, piszemy układ równań w sposób matrycy:

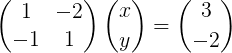Rysunek 2. Układ liniowy w formie macierzy.

Zauważ, że ten system jest zapisany w kompaktowej notacji wektorowej w następujący sposób:

M x = b

Gdzie

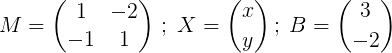
Następnym krokiem jest znalezienie m.

Metoda 1: poprzez eliminację Gaussa

Zastosowana zostanie metoda eliminacji Gaussa. Który polega na wykonywaniu podstawowych operacji w szeregach matrycy, te operacje to:

- Pomnóż wiersz przez liczbę nieskórną.

- Dodaj lub odejmij inny wiersz lub wielokrotność innego wiersza.

- Wymiana wierszy.

Celem jest, dzięki tym operacjom, przekonwertowanie oryginalnej macierzy na macierz tożsamości. 

Jak to się dzieje, w matrycy M stosuje się dokładnie te same operacje do macierzy tożsamości. Gdy po kilku operacjach w wierszach R jest przekształcona w matrycę jednolitą, wówczas ta, która pierwotnie była jednolita, zostanie przekształcona w odwrotną matrycę M, to znaczy m^-1.

Może ci służyć: następstwo (geometria)

1- Rozpoczynamy proces, pisząc matrycę M, a obok niej macierz jednostki:

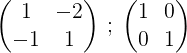
2- Dodajemy dwa wiersze, a wynik jest umieszczony w drugim rzędzie, w ten sposób otrzymujemy zero w pierwszym elemencie drugiego rzędu:

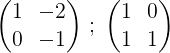
3- Mnożymy drugi wiersz przez -1, aby uzyskać 0 i 1 w drugim rzędzie:

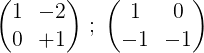
4- Pierwszy rząd jest mnożony przez ½:

5- Drugi i pierwszy dodaje się, a wynik jest umieszczony w pierwszym rzędzie:

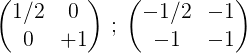
6- Aby zakończyć proces, pierwszy wiersz na 2 jest mnożony, aby uzyskać w pierwszej macierzy tożsamości, aw drugiej macierz odwrotnej oryginalnej macierzy M:

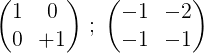
To jest do powiedzenia:

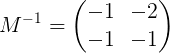
Rozwiązanie systemowe

Po uzyskaniu macierzy odwrotnej układ równań jest rozwiązywany poprzez zastosowanie matrycy odwrotnej w obu członkach kompaktowego równania wektorowego:

M^-1M x = m^-1B

X = m^-1B

To wyraźnie pozostaje takie:

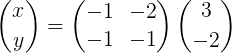
Następnie wykonuje się mnożenie macierzy w celu uzyskania wektora x:

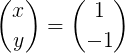
Metoda 2: Za pomocą dołączonej macierzy

W tej drugiej metodzie macierz odwrotnej jest obliczana na podstawie dołączonej macierzy oryginalnej macierzy DO.

Załóżmy, że matryca podana przez:

gdzie_{Ja, J} Jest to element rzędu Siema i kolumna J matrycy DO.

Przywiązanie matrycy DO Zostanie nazywane Przym (a) A jego elementy to:

OGŁOSZENIE_{Ja, J} = (-1)^(i+j) ¦ai, jim

Gdzie Ai, j Jest to uzupełniająca się mniejsza matryca, która jest uzyskiwana przez wyeliminowanie wiersza I i kolumny J z oryginalnej macierzy DO. Słupki ¦ ¦ Wskazują, że wyznacznik jest obliczany, to znaczy ¦ai, jim Jest to wyznacznik uzupełniającej się mniejszej matrycy.

Może ci służyć: homologiczne strony

Odwrotna formuła macierzy

Wzór do znalezienia odwrotnej macierzy oparty na dołączonej macierzy oryginalnej macierzy jest następujący:

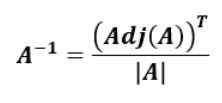
To znaczy odwrotna matryca DO, DO^-1, to transpozycja przywiązania DO podzielone przez determinant DO.

Transponowane DO^Tmacierzy DO Jest to ten uzyskany przez wymianę rang dla kolumn, to znaczy pierwszy wiersz staje się pierwszą kolumną, a drugi wiersz do drugiej kolumny i tak dalej, aż do n wierszy oryginalnej macierzy.

Ćwiczenie rozwiązane

Bądź matrycą do następnej:

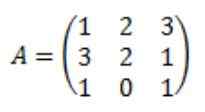
Każdy z elementów dołączonej macierzy A: przym (a) są obliczane

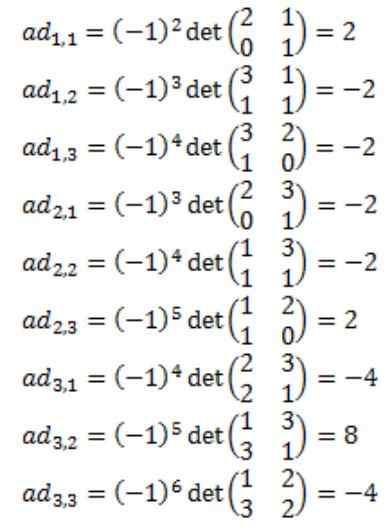
W rezultacie, że dołączona matryca a, przym (a) jest następująca:

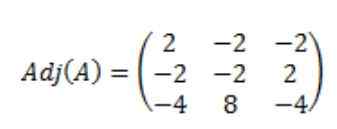
Następnie oblicza się wyznacznik macierzy A, Det (a):

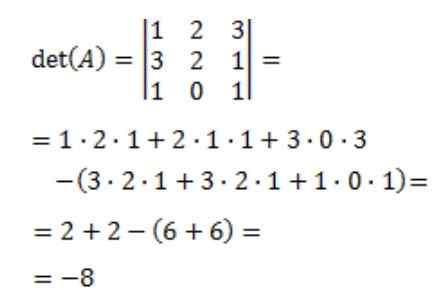
Wreszcie uzyskuje się odwrotną matrycę A:

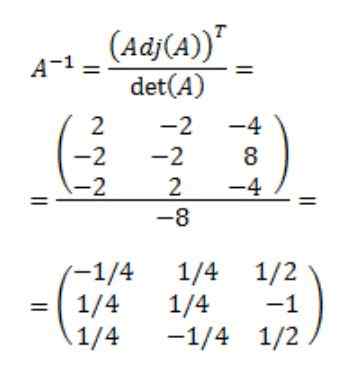
Bibliografia

1. Anthony Nicolaides (1994) Determinanty i macierze. Pokrywanie publikacji.
2. AWOL Assen (2013) Badanie obliczania determinantów 3 × 3
3. Casteleiro Villalba m. (2004) Wprowadzenie do algebry liniowej. ESIC EDYTORIAL.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Maths: A Student's Survival Guide. Cambridge University Press.
6. Richard J. Brown (2012) 30-sekundowe matematyki: 50 najbardziej ekspandujących teorie w matematyce. Ivy Press Limited.
7. Matryca. Lap Lambert Academic Publishing.