Matematyka

Właściwości heptadecágono, przekątne, obwód, obszar

Właściwości heptadecágono, przekątne, obwód, obszar

On heptadecágono Jest to zwykły wielokąt 17 stron i 17 wierzchołków. Jego konstrukcję można wykonać w stylu euklidowskim, to znaczy tylko z użyciem reguły i kompasu. Był to wielki geniusz matematyki Carl Friedrich Gauss (1777–1855), liczący zaledwie 18 lat, który znalazł procedurę budowy w 1796 roku. 

Najwyraźniej Gauss zawsze czuł się bardzo skłonny do tej geometrycznej postaci, do tego stopnia, że ​​od dnia, w którym odkrył swoją konstrukcję, postanowił zostać matematykiem. Mówi się również, że chciał, aby heptadecágono został nagrany na jego nagrobku.

Rysunek 1. Heptadecágono to regularny wielokąt 17 stron i 17 wierzchołków. Źródło: f. Zapata.

Gauss znalazł również formułę ustalenia, które zwykłe wielokąty mają możliwość zbudowania z regułami i kompasem, ponieważ niektórzy nie mają dokładnej konstrukcji euklidesowej.

[TOC]

Charakterystyka heptadecágono

Jeśli chodzi o jego cechy, jak każdy wielokąt, suma jego wewnętrznych kątów jest ważna. W zwykłym wielokąt N boki, suma jest podana przez:

SA (n) = (n -2) *180º.

Dla heptadecágono liczba stron N Jest 17, Co oznacza, że ​​suma jego wewnętrznych kątów to:

SA (17) = (17–2) * 180º = 15 * 180º = 2700º.

Ta suma, wyrażona w Radianach, jest taka:

SA (17) = (17 - 2) * π = 15 * π = 15π

Z poprzednich formuł można łatwo wywnioskować, że każdy wewnętrzny kąt heptadecágono ma dokładną miarę α podaną przez:

α = 2700º/17 = (15/17) π promienia

Wynika z tego, że kąt wewnętrzny jest w przybliżeniu:

α ≈ 158 824º

Piagonals i obwód

Po przekątnej i obwodzie to inne ważne aspekty. W każdym wielokąta liczba przekątnej wynosi: 

D = n (n - 3) / 2 aw przypadku heptadecágono, takiego jak N = 17, Musisz D = 119 Piagonals.

Może ci służyć: trójmian

Z drugiej strony, jeśli znana jest długość każdej strony heptadecágono, to obwód zwykłego heptadecágonu po prostu dodaje 17 razy długość lub co jest równoważne 17 -krotność długości D Po każdej stronie:

P = 17 D

Obwód heptadecágono 

Czasami znane jest tylko radio R heptadecágono, więc konieczne jest opracowanie formuły w tej sprawie.

W tym celu koncepcja Apothem. Apoteme to segment, który przechodzi od środka zwykłego wielokąta do punktu środkowego z jednej strony. Apothem w stosunku do boku jest prostopadłe do tej strony (patrz ryc. 2).

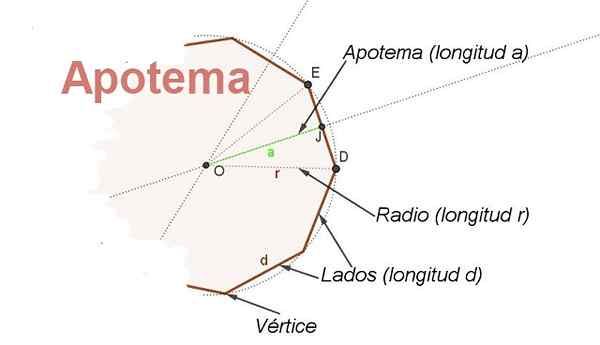Rysunek 2. Pokazane są części zwykłego wielokąta radiowego R i jego apothem. (Własne opracowanie)

Ponadto apothem jest dwusa'a kąta z centralnym wierzchołkiem i bokami na dwóch kolejnych wierzchołkach wielokąta, co pozwala znaleźć związek między radiową R i bok D.

Jeśli się nazywa β pod kąt centralny Łania I biorąc pod uwagę ten apothem OJ Czy masz bisektor Ex = d/2 = r Sen (β/2), gdzie masz związek, aby znaleźć długość D z boku wielokąta znanego radia R i jego centralny kąt β:

D = 2 R sin (β/2)

W przypadku Heptadecágon β = 360º/17 Za to, co masz:

D = 2 R Sen (180º/17) ≈ 0,3675 r

Wreszcie, formuła obwodu heptadecágono, o której wiadomo, że jego promień jest uzyskiwany:

P = 34 R Sen (180º/17) ≈ 6.2475 r

Obwód heptadecágonon Pcir = 2π r ≈ 6.2832 r.

Obszar

Aby określić obszar heptadecágono, będziemy odnosić się do ryc. 2, który pokazuje boki i apothem zwykłego wielokąta N boki. Na tej figurze trójkąt Eod Ma obszar równy podstawie D (strona wielokąta) według wysokości Do (Polygon Apothem) podzielony przez 2:

Może ci służyć: seria mocy: przykłady i ćwiczenia

Eod = (d x a) / 2

Więc ten znany apoteme Do heptadecágono i boku D tego samego jest:

Obszar heptadecágono = (17/2) (d x a)

Obszar podany bok

Aby uzyskać formułę dla obszaru heptadecágono, znając długość jego siedemnastu stron, konieczne jest osiągnięcie związku między długością apothemu Do i bok D.

W odniesieniu do rysunku 2 masz następującą relację trygonometryczną:

Tan (β/ 2) = np./ Oj = (d/ 2)/ a, istnienie β pod kąt centralny Łania. Tak, że apothem Do można obliczyć, jeśli długość jest znana D ze strony wielokąta i kąt centralny β:

A = (d/2) Cotan (β/2)

Jeśli to wyrażenie dla Apothem zostanie teraz zastąpione, w formule obszaru Heptadecágono uzyskanego w poprzedniej sekcji, masz:

Obszar heptadecágono = (17/4) (d2) Cotan (β/2)

Istnienie β = 360º/17 Dla heptadecágono, więc w końcu masz pożądaną formułę:

Obszar heptadecágono = (17/4) (d2) Cotan (180º/17)

Obszar biorąc pod uwagę radio

W poprzednich sekcjach znaleziono związek między stroną D zwykłego wielokąta a jego radiem R, następujące: następujące: następujące::

D = 2 R sin (β/2)

To wyrażenie dla D Jest wprowadzany do wyrażenia uzyskanego w poprzednim rozdziale dla obszaru. Jeśli dokonane są odpowiednie podstawienia i uproszczenia, uzyskano formułę, która pozwala obliczyć obszar heptadecágono:

Obszar heptadecágono = (17/2) (r2) Sin (β) = (17/2) (r2) Sen (360º/17)

Przybliżone wyrażenie dla tego obszaru jest:

Obszar heptadecágono = 3 0706 (r2) 

Zgodnie z oczekiwaniami, obszar ten jest nieco mniejszy niż obszar koła, który ogranicza heptadecágon DOCyrk = π r2 ≈ 31416 r2. Mówiąc dokładniej, jest o 2% niższy niż w ograniczonym okręgu.

Może ci służyć: obszar regularnego i nieregularnego pięciokąta: jak to jest przyjmowane, ćwiczenia

Przykłady

Przykład 1

Aby heptadecágono miał 2 cm, jaka wartość powinna mieć promień i średnica ograniczonego obwodu? Znajdź także wartość obwodu.

Aby odpowiedzieć na pytanie, należy pamiętać o związku między bokiem a promieniem zwykłego wielokąta po bokach:

 D = 2 R Sen (180º / N)

Dla heptadecágono N = 17, stąd D = 0,3675 r, Innymi słowy

O średnicy 10 8844 cm.

Heptadecágon po stronie 2 cm wynosi p = 17* 2 cm = 34 cm.

Przykład 2

Ile kosztuje obszar zwykłej strony heptadecágono de 2 cm?

Konieczne jest odwołanie się do formuły wykazanej w poprzedniej sekcji, która pozwala znaleźć obszar heptadecágono, gdy jest długość D Po jego stronie:

Obszar heptadecágono = (17/4) (d2) / Tan (180º / 17) 

Podczas wymiany D = Uzyskuje się 2 cm w wzorze przednim:

Obszar = 90,94 cm

Bibliografia

  1. C. I. DO. (2003). Elementy geometrii: z ćwiczeniami i geometrią kompasu. University of Medellin.
  2. Campos, f., Cerecedo, f. J. (2014). Matematyka 2. Grupa redakcyjna Patria.
  3. Freed, k. (2007). Odkryj wielokąty. Benchmark Education Company.
  4. Hendrik, v. (2013). Uogólnione wielokąty. Birkhäuser.
  5. Iger. (S.F.). Matematyka pierwszy semestr Tacaná. Iger.
  6. Jr. Geometria. (2014). Wielokąty. Lulu Press, Inc.
  7. Miller, Heeren i Hornsby. (2006). Matematyka: rozumowanie i aplikacje (wydanie dziesiąta). Edukacja Pearsona.
  8. Patiño, m. (2006). Matematyka 5. Progreso redakcyjne.
  9. Sada, m. Regularne 17 stron z regułą i kompasem. Odzyskany z: Geogebra.org
  10. Wikipedia. Heptadecágono. Odzyskane z: jest.Wikipedia.com