Charakterystyka elipsoidów i przykłady

On elipsoida Jest to powierzchnia w przestrzeni należącej do grupy powierzchni czterorskich i którego ogólne równanie jest formy:

Topór² + Przez² + CZ² + DXY + EXZ + FYZ + GX + HY + IZ + J = 0

Jest to trójwymiarowy odpowiednik elipsy, charakteryzujący się śladami eliptycznymi i okrągłymi w niektórych szczególnych przypadkach. Ślady to krzywe uzyskiwane podczas przecinania elipsoidy za pomocą płaszczyzny.

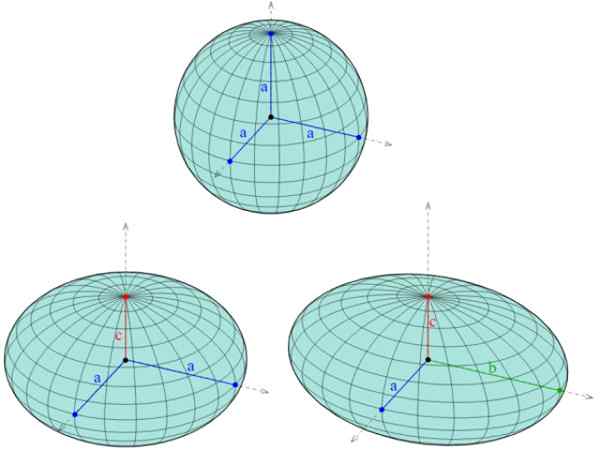
Rysunek 1. Trzy różne elipsoidy: powyżej kuli, w której trzy pół -semi są takie same, do lewej sferoidy, z dwiema równi pół -jednej półki i wreszcie w prawo, trójosiowy sferoid, z trzema osiami o różnej długości. Źródło: Wikimedia Commons. AG2GAEH/CC BY-S (https: // creativeCommons.Org/licencje/nabrzeże/4.0)

Oprócz elipsoidów istnieje pięć innych czterokrotnych: hiperboloid jednego liścia i dwóch liści, dwa rodzaje paraboloidów (hiperboliczne i eliptyczne) i stożka eliptyczne. Jego ślady są również stożkowe.

Elipsoida może być również wyrażona przez standardowe równanie we współrzędnych kartezjańskich. Elipsoid skupił się na pochodzeniu (0,0,0) i wyrażony w ten sposób, przypomina elipsę, ale z dodatkowym terminem:

Wartości Do, B I C Są liczbami rzeczywistymi większymi niż 0 i reprezentują trzy elipsoidowe połowę.

[TOC]

Charakterystyka elipsoidów

- Standardowe równanie 

Standardowe równanie we współrzędnych kartezjańskich dla elipsy skupionych na punkcie (H, K, M) Jest:

- Elipsoid Parametryczne równania

We współrzędnych sferycznych elipsoidy można opisać w następujący sposób:

x = sin θ. cos φ

y = b sin θ. sin φ

Z = C cos θ

Elipsoid Semi -Out nadal to A, B i C, podczas gdy parametry są kątami θ i φ poniższego rysunku:

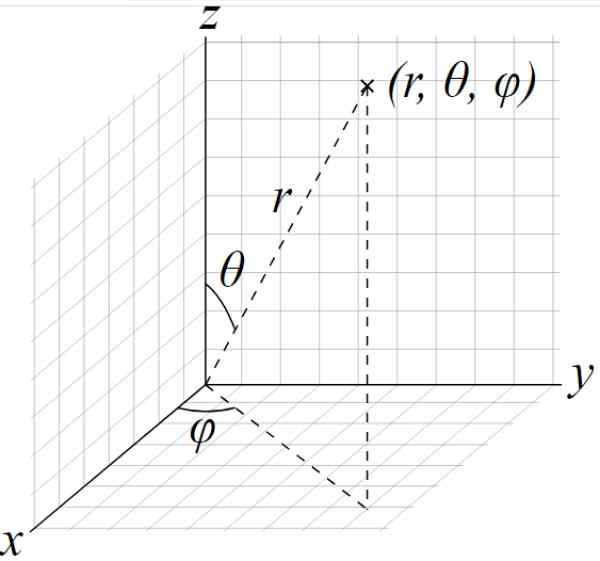Rysunek 2. Sferyczny układ współrzędnych. Elipsoida można sparametryzować przy użyciu kątów pokazanych theta i pHI jako parametry. Źródło: Wikimedia Commons. Domena Anggs / Pub.

- Elipsoid ślady

Ogólne równanie powierzchni w przestrzeni to F (x, y, z) = 0, a ślady powierzchni są krzywe:

Może ci służyć: wielkość wektora

- x = c; F (C, Y, z) = 0

- y = c; F (x, c, z) = 0

- Z = C; F (x, y, c) = 0

W przypadku elipsoidy takie krzywe są elipsami, a czasem obwodami.

- Tom

Objętość V elipsoidy jest podawana przez (4/3) π razy iloczyn trzech półsemi:

V = (4/3) π. ABC

Specjalne przypadki elipsoidów

-Elipsoida staje się kulą, gdy wszystkie połowy -rozmiar tego samego rozmiar. Ma to sens, ponieważ elipsoida jest jak kula, do której była rozciągnięta inaczej w każdej osi.

-Sferoida jest elipsoidą, w której dwa półki są identyczne, a trzecia jest inna, na przykład może to być a = b ≠ c.

Sferoida jest również nazywana elipsoidą rewolucyjną, ponieważ można go generować przez obracanie elipsy wokół osi.

Jeśli oś skrętu pokrywa się z główną osą, sferoid jest prolicja, Ale jeśli zbiega się to z mniejszą osą, tak jest oblat:

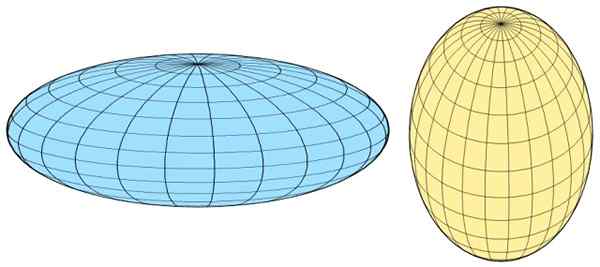Rysunek 3. Sferoida lewej po lewej i prolicja sferoidów po prawej stronie. Źródło: Wikimedia Commons.

Miara spłaszczania sferoidów (eliptyczność) jest podana przez różnicę długości między dwiema półprzewodnikami, wyrażoną w postaci ułamkowej, to znaczy jest spłaszczenie jednostki, podane przez:

F = (a - b) / a

W tym równaniu A reprezentuje półsenije i B mniejszą osi półprzepamiętaj, że trzecia oś jest równa dowolnej z nich dla sferoidy. Wartość F wynosi od 0 do 1, a dla sferoidy musi być większa niż 0 (gdyby była równa 0, po prostu mielibyśmy kulę).

Może ci służyć: Bethelgeuse

Referencyjny elipsoid

Planety i ogólnie gwiazdy nie są zwykle doskonałymi sferami, ponieważ ruch obrotu wokół swoich osi płaski ciało w biegunach i basinałach w Ekwadorze.

Właśnie dlatego Ziemia okazuje się jak oblate sferoidy, choć nie tak przesadzona jak z poprzedniej postaci, a z drugiej strony Giant Saturna jest najbardziej gorzki z planet w Układzie Słonecznym.

Tak więc bardziej realistycznym sposobem reprezentowania planet jest założenie, że są one jak sferoida lub elipsoid rewolucji, której pół -mamor jest radio równikowe i mniejszy półkas polarny promień polarny.

Staranne środki dokonane na świecie pozwoliły na zbudowanie Elipsoid referencyjny Ziemi jako najbardziej precyzyjnej formy do pracy matematycznej.

Gwiazdy mają również ruchy rotacyjne, które nadają im mniej lub bardziej spłaszczone formy. Szybka gwiazda Aternar, ósma najzdolniejsza gwiazda na nocnym niebie, w południowej konstelacji Eridanus jest niezwykle eliptyczna, porównując ją z większością. To 144 lata świetlne od nas.

Z drugiej strony, kilka lat temu naukowcy dali najbardziej sferycznym obiektowi znalezionym do tej pory: gwiazda Keplera 11145123, 5000 lat świetlnych, z wielkością dwa razy większą niż w naszym słońcu i różnicą między półminsagami zaledwie 3 km. Zgodnie z oczekiwaniami, obraca się również wolniej.

Jeśli chodzi o ziemię, nie jest idealnym sferoidem ze względu na jej nierówną powierzchnię i lokalne odmiany grawitacji. Dlatego istnieje więcej niż jeden dostępny sferoida referencyjna i na każdej witrynie wybrano najbardziej odpowiednie dla lokalnej geografii.

Może ci służyć: jaka jest dolina w fizyce? (Z przykładami)

Pomoc satelitów jest nieoceniona w tworzeniu coraz bardziej precyzyjnych modeli kształtu ziemi, dzięki im wiadomo na przykład, że biegun południowy jest bliżej Ekwadoru niż biegun północny.

Rysunek 4. Haumea, transneptunijska planeta krasnoludów ma kształt elipsoidalny. Źródło: Wikimedia Commons.

Przykład liczbowy

Z powodu obrotu Ziemi generowana jest siła odśrodkowa, która nadaje mu formę podłużnej elipsoidy, zamiast kuli. Wiadomo, że radio równikowe Ziemi ma 3963 mil, a promień polarny wynosi 3942 mil.

Znajdź równanie śladu równikowego, równania tej elipsoidy i miary jego spłaszczenia. Porównaj także z eliptycznością Saturna, z danymi podanymi poniżej:

-Radio równikowe Saturn: 60268 km

-Saturn Polar Radio: 54364 km

Rozwiązanie

Wymagany jest układ współrzędnych, który założymy na pochodzeniu (centrum Ziemi). Zakładamy pionową oś Z, a ślad odpowiadający równikowi znajduje.

W płaszczyźnie równikowej pół -A i B są takie same, dlatego A = B = 3963 mil, podczas gdy C = 3942 mil. Jest to szczególny przypadek: sferoida skupiona na punkcie (0,0,0), jak stwierdzono powyżej.

Ślad równikowy to okrąg o promieniu r = 3963 mil, skupiony na pochodzeniu. Oblicza się go, wykonując z = 0 w równaniu standardowym:

A standardowe równanie elipsoidy Ziemi jest:

Wreszcie, miara regulacji (eliptyczna) jest obliczana oceniając w równaniu:

F _Grunt = (a - b) / a = (3963-3942) mil / 3963 mil = 0.0053

F _Saturn = (60268-54363) km/60268 km = 0.0980

Zauważ, że eliptyczna f jest bezwymiarową ilością.

Bibliografia

1. ArcGIS na komputer stacjonarny. Sferoidy i kule. Odzyskany z: komputer stacjonarny.Arcgis.com.
2. BBC World. Tajemnica najbardziej sferycznego obiektu, jakie kiedykolwiek odkryto we wszechświecie. Źródło: BBC.com.
3. Larson, r. Obliczenia i geometria analityczna. Szósta edycja. Głośność 2. McGraw Hill.
4. Wikipedia. Elipsooid. Źródło: w:.Wikipedia.org.
5. Wikipedia. Siperoid. Źródło: w:.Wikipedia.org.