Formuła równań pierwszej klasy, jak je rozwiązać, przykład, ćwiczenia

Równania pierwszego stopnia lub liniowe Z nieznanym są te, które można wyrazić jako sumę dwóch terminów w następujący sposób:

AX + B = 0

Gdzie a i b, z Do ≠ 0, są liczbami rzeczywistymi r lub również kompleksy c. Aby go rozwiązać, warunki są transponowane, co oznacza zmianę warunków z jednej strony na drugą równość.

Rysunek 1. Równanie liniowe to y = mx + c forma z y = 0. Źródło: Pxhere.

Aby wyczyścić nieznane, termin +B jest transponowany, który musi przejść na prawą stronę równości ze zmienionym znakiem.

ax = -B

Następnie wartość x jest oczyszczona w ten sposób:

x = - b/a

Jako przykład rozwiążemy następujące równanie:

6x - 5 = 4

Przetrzymujemy termin -5 po prawej stronie ze zmienionym znakiem:

6x = 4 + 5

Jest to równoważne dodawaniu 5 po obu stronach pierwotnego równania:

6x - 5 + 5 = 4 + 5 → 6x = 9

A teraz wyczyścimy nieznany „x”:

x = 9/6 = 3/2

Co jest równoważne podzieleniu obu stron równości przez 6. Mamy więc ocenić następujące informacje, aby uzyskać rozwiązanie:

-Tę samą kwotę można dodać lub odjąć obie strony równości w równaniu, bez zmiany.

-Możesz także pomnożyć (lub podzielić) przez tę samą kwotę na wszystkie warunki zarówno po lewej, jak i po prawej stronie równania.

-A jeśli obaj członkowie równania wzrośnie do tej samej mocy, równość też nie zostanie zmieniona.

[TOC]

Jak rozwiązać równania pierwszego stopnia

Rozwiązanie równania pierwszego stopnia jest również znane jako korzeń tego samego. Jest to wartość x, która przekształca oryginalne wyrażenie w równość. Na przykład w:

5x = 8x - 15

Jeśli zastąpimy x = 5 w tym równaniu, jest on uzyskiwany:

5⋅5 = 8⋅5 - 15

25 = 40 - 15

25 = 25

Ponieważ liniowe równania pierwszego stopnia pojawiają się na wiele sposobów, które czasami nie są widoczne, istnieje szereg ogólnych zasad, które obejmują kilka manipulacji algebraicznych, aby znaleźć wartość nieznanego:

-Po pierwsze, jeśli wskazane są operacje, należy je przeprowadzić.

-Grupowanie symboli, takich jak nawiasy, nawiasy kwadratowe i klucze, jeśli istnieją, muszą zostać stłumione, utrzymując odpowiednie znaki.

-Warunki są transponowane, aby umieścić wszystkie te, które zawierają nieznane jednej stronie równości, a te, które nie zawierają go na drugim.

-Wtedy wszystkie podobne terminy są zmniejszone, aby osiągnąć formularz ax = -B.

-A ostatnim krokiem jest wyczyszczenie nieznanego.

Interpretacja graficzna

Równanie pierwszego stopnia podniesione na początku można wyprowadzić z równania linii y = mx+c, robiąc y = 0. Wartość x, która wyniki odpowiada przecięciu linii z osą poziomą.

Na poniższej liczbie masz trzy linie. Zaczynając od zielonej linii, której równanie to:

Może ci służyć: czynnikowanie

y = 2x - 6

Wykonanie y = 0 w linii linii uzyskuje się równanie pierwszego stopnia:

2x - 6 = 0

Którego rozwiązanie to x = 6/2 = 3. Teraz, gdy szczegółowo opisujemy wykres, łatwo uświadomić sobie, że w efekcie linia przecina osi poziomej przy x = 3.

Niebieska linia przecina oś x przy x = 5, co jest rozwiązaniem równania -x + 5 = 0. Wreszcie linia, której równanie to y = 0.5x + 2 Przecięcie osi x przy x = -4, co można łatwo ostrzegać przed równaniem pierwszego stopnia:

0.5 x + 2 = 0

x = 2/0.5 = 4

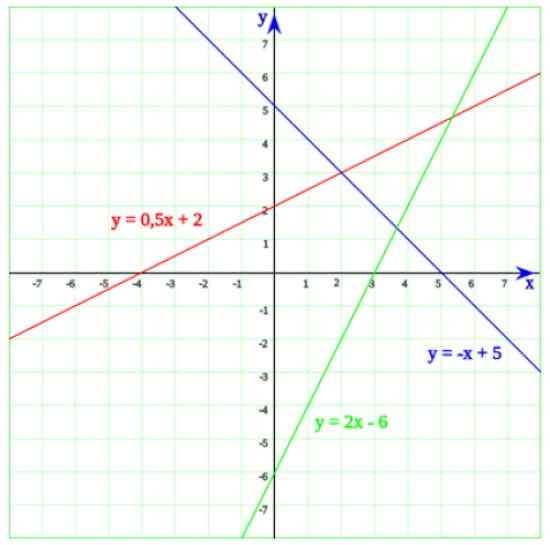Rysunek 2. Trzy linie, których przecięcia z osą poziomą odpowiadają równaniom liniowym. Źródło: Wikimedia Commons.

Przykłady prostych równań liniowych   

Całe równania

Są tymi, w których na przykład nie ma mianowników, na przykład:

21 - 6x = 27 - 8x

Jego rozwiązaniem jest:

-6x + 8x = 27 - 21

2x = 6

x = 3

Równania ułamkowe

Równania te zawierają co najmniej jeden inny mianownik 1. Aby je rozwiązać, jest to wskazane.

Poniższe równanie to typ ułamkowy:

Mianowniki to 6, 8 i 12, a ich minimalna wspólna wielokrotność, oznaczona jako m.C.M (6, 8,12) to najmniejsza liczba zawierająca te mianowniki.

Ponieważ liczby te są małe, nietrudno zauważyć, że m.C.M (6, 8,12) = 24. Ten wynik można łatwo uzyskać, wyrażając liczby jako produkt liczb pierwszych lub ich mocy, zobaczmy:

6 = 3.2

8 = 2³

12 = 2²⋅3

Minimalna wspólna wielokrotność jest określana przez pomnożenie wspólnych i niekommonowych czynników 6, 8 i 12 z jego największym wykładnikiem:

MCM (6,8,12) = 2³ ⋅3 = 8 × 3 = 24

Ponieważ dostępna jest minimalna wspólna wielokrotność, należy ją pomnożyć przez każdy z warunków równania:

W ten sposób mianowniki są tłumione i istnieje równanie z produktami, łatwiejsze do rozwiązania:

4 (x+5) -3 (2x+3) = 2 (1-5x)

Korzystamy z nieruchomości dystrybucyjnych:

4x + 20 - 6x -9 = 2 - 10x

Wszystkie terminy zawierające nieznane „x” są pogrupowane po lewej stronie równości, pozostawiając niezależne lub numeryczne warunki prawej strony:

4x - 6x + 10 x = 2 +9 - 20

8x = -9

x = - 9/8

Dosłowne równania

Są to równania liniowe z nieznanym, którym jednak towarzyszy dosłowne współczynniki (litery). Te litery są traktowane tak, jak to możliwe z liczbami. Przykładem dosłownego równania pierwszego stopnia jest:

-3ax + 2a = 5x - b

To równanie jest rozwiązane w taki sam sposób, jakby niezależne warunki i współczynniki były numeryczne:

-3AX - 5x = - B - 2a

Uwzględnianie nieznanego „x”:

x (-3a - 5) = - b - 2a

x = ( - b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)

Systemy równań pierwszego stopnia 

Systemy równań składają się z zestawu równań z dwoma lub więcej niewiadomymi. Rozwiązanie systemowe składa się z wartości, które spełniają równania jednocześnie i aby ustalić je jednoznacznie, musi istnieć równanie dla każdego niewiadomych.

Może ci służyć: algebra wektorowa

Ogólna forma systemu M Równania liniowe z N Nieznane są:

Do_jedenaścieX₁ + Do₁₂X₂ +… Do_1nX_N = b₁
Do_{dwadzieścia jeden}X₁ + Do₂₂X₂ +… Do_2nX_N = b₂
..
Do_M1X₁ + Do_M2X₂ +… Do_MnX_N = b_M

Jeśli system ma rozwiązanie, mówi się, że tak jest określony kompatybilny, Gdy istnieje nieskończony zestaw wartości, który to zaspokoi nieokreślony kompatybilny, I wreszcie, jeśli nie ma rozwiązania, to jest niekompatybilny.

W rozdzielczości systemów równań liniowych stosuje się kilka metod: redukcja, wymiana, wyrównanie, metody graficzne, eliminacja Gaussa-Jordanu i zastosowanie determinantów należą do najczęściej używanych. Ale istnieją inne algorytmy do osiągnięcia rozwiązania, wygodniejsze dla systemów z wieloma równaniami i niewiadomymi.

Przykładem układu równań liniowych z dwoma niewiadomymi jest:

8x - 5 = 7Y - 9
6x = 3y + 6

Rozwiązanie tego systemu jest przekazywane później w sekcji rozwiązanych ćwiczeń.

Równania liniowe o wartości bezwzględnej

Wartość bezwzględna liczby rzeczywistej to odległość między jej lokalizacją na linii liczbowej a 0 tego samego. Bycie w pewnej odległości, jego wartość jest zawsze pozytywna.

Wartość bezwzględna liczby jest oznaczona przez słupki modułu: │x│. Na przykład wartość bezwzględna liczby dodatniej lub ujemnej jest zawsze pozytywna:

│+8│ = 8

│-3│ = 3

W równaniu o wartości bezwzględnej nieznana jest między słupkami modułów. Rozważ następujące proste równanie:

│x│ = 10

Istnieją dwie możliwości, po pierwsze, X jest liczbą dodatnią, w którym to przypadku mamy:

x = 10

A inną możliwością jest to, że X jest liczbą ujemną, w tym przypadku:

x = -10

Są to rozwiązania tego równania. Teraz zobaczmy inny przykład:

│x+6│ = 11

Kwota w słupkach może być pozytywna, zatem:

x+6 = 11

x = 11 -6 = 5

Lub może być negatywne. W tym wypadku:

-(x+6) = 11

-x - 6 = 11 ⇒ -x = 11+6 = 17

A wartość nieznanego to:

x = -17

To równanie wartości bezwzględnej ma zatem dwa rozwiązania: x₁ = 5 i x₂ = -17. Możemy sprawdzić, czy oba rozwiązania prowadzą do równości w oryginalnym równaniu:

│5+6│ = 11

│11│ = 11

I

│-17+6│ = 11

│-11│ = 11

Proste rozwiązane ćwiczenia

- Ćwiczenie 1

Rozwiąż następujący układ równań liniowych z dwoma niewiadomymi:

8x - 5 = 7y -9
6x = 3y + 6

Rozwiązanie

Gdy ten system jest podniesiony, jest odpowiedni do stosowania metody zastępowania, ponieważ w drugim równaniu nieznane X Jest prawie gotowy do prześwitu:

x = (3y + 6)/6

Może ci służyć: algebraiczna

I możesz natychmiast wymienić pierwsze równanie, które następnie staje się pierwszym równaniem o nieznanym „y”:

8 [(3y + 6)/6] - 5 = 7y - 9

Mianownik można stłumić, jeśli każdy termin jest mnożony przez 6:

6 . 8⋅ [(3y + 6)/6] - 6.5 = 6 .7Y- 6 . 9

8⋅ (3y + 6) - 30 = 42Y - 54

Stosowanie nieruchomości dystrybucyjnej w pierwszym okresie na prawo do równości:

24y + 48 -30 = 42Y - 54 ⇒ 24y + 18 = 42Y - 54

Równanie można uprościć, ponieważ wszystkie współczynniki mają wielokrotności 6:

4y + 3 = 7y - 9

-3y = -12

y = 4

Z tym wynikiem przechodzimy do prześwitu x:

x = (3y +6)/6 → x = (12 +6)/6 = 3

- Ćwiczenie 2

Rozwiąż następujące równanie:

Rozwiązanie

W tym równaniu pojawiają się produkty i postępując zgodnie z instrukcjami podanymi na początku, należy je najpierw opracować:

3x - 10x +14 = 5x + 36x + 12

Wówczas wszystkie terminy zawierające niewiadome są przenoszone na lewą stronę równości, a po prawej stronie niezależne terminy będą:

3x - 10x - 5x - 36x = 12–14

-48x = -2

x = 1/24

- Ćwiczenie 3

Dodając trzy kąty wewnętrzne trójkąta, otrzymuje się 180º. Największe przekracza dziecko w 35º, a to z kolei przekracza w 20º różnica między największym i średnim. Jakie są kąty?

Rozwiązanie

Nazwimy „X” pod głównym kątem, „Y” do medium i „Z” do dziecka. Kiedy stwierdzenie stwierdza, że ​​ich suma wynosi 180º, możesz napisać:

x + y + z = 180

Następnie wiemy, że najstarszy przekracza dziecko w 35º, możemy to napisać:

X = z + 35

Wreszcie dziecko przekracza 20 ° Cu różnicę między największym a medium:

Z = x - y + 20

Mamy układ 3 równań i 3 niewiadomy:

x + y + z = 180

X = z + 35

Z = x - y + 20

Oczyszczając pierwsze równanie, masz:

Z = 180 - x - y

Dopasowanie trzeciego:

180 - x - y = x - y + 20

Jak zawsze przekazywanie niewiadomych na lewą stronę:

-x - y - x + y = 20 - 180

„Y” jest anulowane i pozostaje:

-2x = - 160

x = 80º

Drugie równanie to wartość Z:

Z = x - 35 = 80–35 = 45º

Oraz wartość i jest pierwsza lub trzeci:

y = 180 - x - z = 180 - 80 - 45 = 55º

Bibliografia

1. Baldor. 1977. Algebra podstawowa. Wenezuelskie wydania kulturalne.
2. Monterey Institute. Równania, nierówności i wartość bezwzględna. Odzyskane z: Montereyinstitute.org.
3. Nauczyciel online. Klasyfikacja równań liniowych lub pierwszych. Odzyskane od: profesor Inline.Cl.
4. Hoffman, J. Wybór problemów z matematyką. Głośność 2.
5. Jiménez, r. 2008. Algebra. Prentice Hall.
6. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.