Cylindryczne współrzędne systemu, zmiany i ćwiczenia

Współrzędne cylindryczne Służą do zlokalizowania punktów w trójwymiarowej przestrzeni i składają się z współrzędnej promieniowej ρ, współrzędnej azymutowej φ i współrzędnej wysokości z.

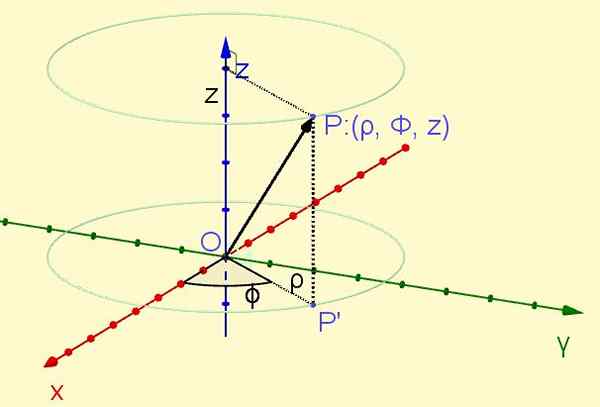
Punkt P Położone w kosmosie jest rzutowane ortogonalnie w samolocie Xy dbanie o sedno P ' W tej płaszczyźnie. Odległość od pochodzenia do punktu P ' definiuje współrzędną ρ, podczas gdy kąt, który tworzy oś X Z półprzestrzennym OP ' Zdefiniuj współrzędną φ. Wreszcie współrzędna z Jest to ortogonalna projekcja punktu P na osi Z. (Patrz rysunek 1).

Rysunek 1. Punkt p cylindrycznych współrzędnych (ρ, φ, z). (Własne opracowanie)

Współrzędna promieniowa ρ jest zawsze dodatnia, współrzędna azymutalna φ zmienia się od zerowych radian do dwóch radian pi, podczas gdy współrzędna Z może przyjąć dowolną wartość rzeczywistą:

0 ≤ ρ < ∞

0 ≤ φ < 2π

- ∞ < z < + ∞

[TOC]

Zmiana współrzędnych

Uzyskanie współrzędnych kartezjańskich (x, y, z) jest stosunkowo proste z punktu P od jego cylindrycznych współrzędnych (ρ, φ, z):

x = ρ cos (φ)

y = ρ sen (φ)

Z = z

Ale możliwe jest również uzyskanie współrzędnych polarnych (ρ, φ, z) na podstawie wiedzy współrzędnych kartezjańskich (x, y, z) punktu p:

ρ = √ (x² + I²)

φ = arctan (y/x)

Z = z

Podstawa wektorowa we współrzędnych cylindrycznych

Zdefiniowana jest podstawa cylindrycznych wektorów Uρ, Uφ, Uz.

Wektor Uρ Jest styczny do linii φ = ctte i z = ctte (wskazujący promieniowo), wektor Uφ jest styczna do linii ρ = ​​ctte i z = ctte i na koniec Uz Ma ten sam kierunek osi Z.

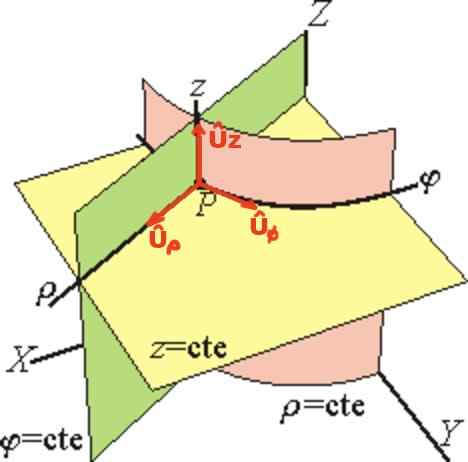Rysunek 2. Cylindryczna podstawa współrzędnych. (Wikimedia Commons)

W cylindrycznej podstawie jednostki wektor położenia R Od punktu P jest napisane wektorowo tak:

Może ci służyć: domena i sprzeczność funkcji (z przykładami)

R = ρ Uρ + 0 Uφ + z Uz

Z drugiej strony, nieskończenie małe przemieszczenie dR Od punktu P wyraża się następująco:

DR = Dρ Uρ + ρ dφ  Uφ + Dz Uz

Podobnie, nieskończenie małym objętości DV we współrzędnych cylindrycznych jest:

Dv = ρ dρ dφ dz

Przykłady

Istnieje niezliczone przykłady zastosowania i zastosowania współrzędnych cylindrycznych. Na przykład w kartografii rzut cylindryczny, oparte dokładnie na tych współrzędnych. Jest więcej przykładów:

Przykład 1

Cylindryczne współrzędne mają zastosowania w technologii. Jako przykład masz system danych CHS (sektor cylindra) na dysku twardym, który w rzeczywistości składa się z kilku dysków:

- Cylinder lub tor odpowiada współrzędnej ρ.

- Sektor odpowiada pozycji φ albumu, która obraca się na wysokim poziomie prędkość kątowa.

- Głowa odpowiada pozycji Z czytania na odpowiednim albumie.

Każdy bajt informacyjny ma precyzyjny adres we współrzędnych cylindrycznych (C, S, H).

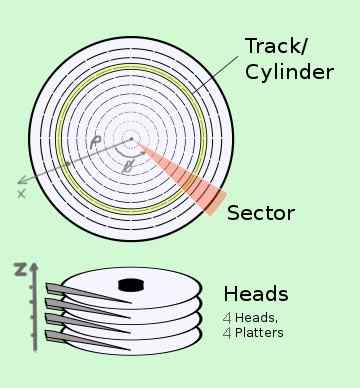Rysunek 2. Lokalizacja informacji we współrzędnych cylindrycznych w systemie dysku twardego. (Wikimedia Commons)

Przykład 2

Żuty budowlane ustawiają pozycję obciążenia we współrzędnych cylindrycznych. Pozycja pozioma jest zdefiniowana przez odległość do osi dźwigu lub strzałki. Pionowa pozycja obciążenia jest określona przez współrzędną Z wysokości.

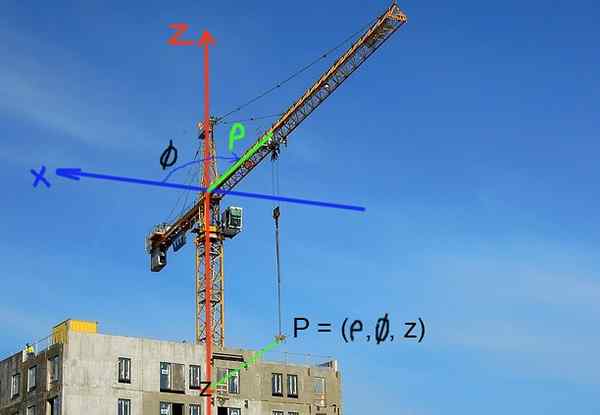Rysunek 3. Położenie obciążenia w dźwigu konstrukcyjnym można łatwo wyrazić we współrzędnych cylindrycznych. (Pixabay Image - RCOS R. Pérez)

Rozwiązane ćwiczenia

Ćwiczenie 1

Istnieją punkty P1 współrzędnych cylindrycznych (3, 120º, -4) i punkt P2 współrzędnych cylindrycznych (2, 90º, 5). Znaleźć Odległość euklidyjska Między tymi dwoma punktami.

Może ci służyć: podziały, w których pozostałość wynosi 300

Rozwiązanie: Najpierw znaleźliśmy współrzędne kartezjańskie każdego punktu po wzorze, które wystąpiły powyżej.

P1 = (3* cos 120º, 3* Sen 120º, -4) = (-1.5, 2.60, -4)

P2 = (2* cos 90º, 2* sin 90º, 5) = (0, 2, 5)

Odległość euklidyjska między P1 i P2 to:

D (p1, p2) = √ ((0 - (-1.5))²+(2 - 2.60)²+(5 -(-4))² ) =…

… √ (2.25+0.36+81) = 9.14

Ćwiczenie 2

Point P ma współrzędne kartezjańskie (-3, 4, 2). Znajdź odpowiednie współrzędne cylindryczne.

Rozwiązanie: Cylindryczne współrzędne znajdują się przy użyciu relacji podanych powyżej:

ρ = √ (x² + I²) = √ ((-3)² + 4²) = √ (9 + 16) = √ (25) = 5

φ = arctan (y/x) = arcan (4/(-3)) = -53.13º + 180º = 126.87º

Z = 2

Należy pamiętać, że funkcją łukowatą jest multiviluada okresowości 180º. Ponadto kąt φ musi należeć do drugiego kwadrantu, ponieważ współrzędne x e y i punktu p znajdują się w tej ćwiartce. To jest powód, dla którego do wyniku dodano 180º.

Ćwiczenie 3

Ekspresja we współrzędnych cylindrycznych i współrzędnych kartezjańskich powierzchni cylindra radiowego 2 i której osi pokrywa.

Rozwiązanie: Rozumie się, że cylinder ma nieskończone przedłużenie w kierunku Z, tak że równanie wspomnianej powierzchni we współrzędnych cylindrycznych wynosi:

ρ = 2

Aby uzyskać równanie kartezjańskie powierzchni cylindrycznej, pobrany jest kwadrat obu członków poprzedniego równania:

ρ² = 4

Mnożymy się przez 1 obaj członkowie poprzedniej równości i stosujemy Podstawowa tożsamość trygonometryczna (Sen²(φ) + cos²(φ) = 1):

1 * ρ² = 1 * 4

(Sen²(φ) + cos²(φ)) * ρ² = 1 * 4

W celu uzyskania nawiasów:

(ρ Sen (φ))² + (ρ cos (φ))² = 4

Może ci służyć: populacja i próbka

Pamiętamy, że pierwszy nawias (ρ Sen (φ)) jest współrzędna i punktem współrzędnym polarnym, podczas gdy nawias (ρ cos (φ)) reprezentuje współrzędną x, więc zostawiliśmy Równanie cylindra we współrzędnych kartezjańskich:

I² + X² = 2²

Poprzedniego równania nie należy mylić z równaniem okręgu w płaszczyźnie XY, ponieważ w tym przypadku byłoby tak: i² + X² = 2² ; Z = 0.

Ćwiczenie 4

Cylinder o promieniu r = 1 mi wysokość H = 1M ma swoją promieniowo rozłożoną masę zgodnie z następującym równaniem D (ρ) = C (1 - ρ/r), gdzie C jest stałą wartości c = 1 kg/m³. Znajdź całkowitą masę cylindra w kilogramach.

Rozwiązanie: Pierwszą rzeczą jest uświadomienie sobie, że funkcja D (ρ) reprezentuje gęstość masy objętościowej i że masa gęstości jest rozmieszczona w cylindrycznych kaskaronach o zmniejszającej gęstości środka na peryferie. Nieskończonym elementem objętości według symetrii problemu jest:

Dv = ρ dρ 2π h

Stamtąd musisz, nieskończona masa cylindrycznej powłoki będzie:

DM = D (ρ) DV

Tak więc całkowita masa cylindra zostanie wyrażona przez następujące Zdefiniowana całka:

M = ∫_albo^R D (ρ) dv = ∫_albo^R C (1 - ρ/r) ρ dρ 2π H = 2π H C ∫_albo^R (1 - ρ/r) ρ dρ

Rozwiązanie wskazanej całki nie jest trudne do uzyskania, ponieważ jego wynik:

∫_albo^R (1 - ρ/r) ρ dρ = (⅙) r²

Uwzględniono ten wynik w ekspresji masy cylindra:

M = 2π H C (⅙) R² = ⅓ π h c r² =

 ⅓ π 1m*1 kg/m³* 1m² = π/3 kg ≈ 1.05 kg

Bibliografia

1. Arfken G i Weber H. (2012). Metody matematyczne dla fizyków. Kompleksowy przewodnik. 7. edycja. Academic Press. ISBN 978-0-12-384654-9
2. Obliczenie CC. Rozwiązane współrzędne cylindryczne i sferyczne. Odzyskane z: Obliczanie.DC
3. Weisstein, Eric W. „Cylindryczne współrzędne.”Z Mathworld-A Wolfram Web. Odzyskane z: Mathworld.Wolfram.com
4. Wikipedia. Cylindryczny układ współrzędnych. Źródło: w:.Wikipedia.com
5. Wikipedia. Pola wektorowe we współrzędnych cylindrycznych i sferycznych. Źródło: w:.Wikipedia.com