Matematyka

Zgodność zgodna z postaciami, kryteriami, przykładami, ćwiczeniami

Zgodność zgodna z postaciami, kryteriami, przykładami, ćwiczeniami

stosowność, W geometrii wskazuje, że jeśli dwie płaskie postacie mają tę samą formę i wymiary, są one zgodne. Na przykład dwa segmenty są zgodne, gdy ich długości są równe. Również przystające kąty mają tę samą miarę, chociaż nie są zorientowane w ten sam sposób w samolocie.

Termin „zgodność” pochodzi z łaciny Congruentia, którego znaczenie jest korespondencją. Zatem dwie przystające liczby odpowiadają dokładnie jednemu z drugim.

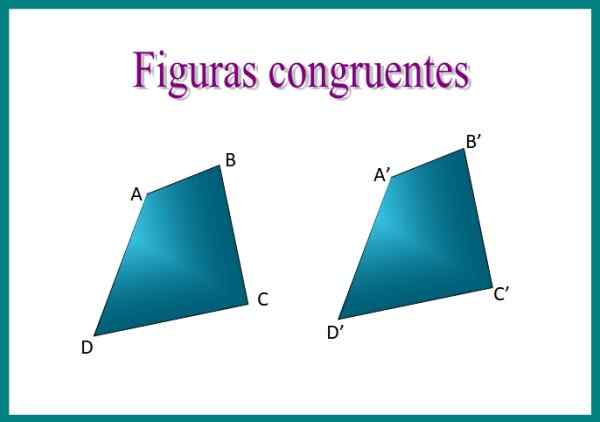
Rysunek 1. Czworobok Abcd i a'b'c'd z tej postaci są zgodne: ich boki mają tę samą miarę, a także ich wewnętrzne kąty. Źródło: f. Zapata.

Na przykład, jeśli nakładamy się na dwa czworobok obrazu, przekonamy się, że są one zgodne, ponieważ rozmieszczenie ich boków jest identyczne i mierzą to samo.

Podczas umieszczania czworoboku abcd i a'b'c'd „na drugim, liczby będą dokładnie pokryć. Dopasowane strony są nazywane Homologiczne strony albo odpowiedni I aby wyrazić zgodność, używany jest symbol ≡. Następnie możemy powiedzieć, że abcd ≡ a'b'c'd '.

[TOC]

Kryteria zgodności

Następujące cechy są wspólne dla przystających wielokątów:

-Równy kształt i rozmiar.

-Identyczne miary twoich kątów.

-W tym samym zasięgu po każdej ze stron.

W przypadku, gdy dwa, o których mowa, są regularne, to znaczy, że wszystkie strony i kąty wewnętrzne mierzą to samo, zgodność jest zapewniona, gdy spełnione jest jeden z poniższych warunków:

-Strony są zgodne

- Apothems mieć tę samą miarę

-On radio każdego wielokąta mierzy to samo

Apoteme zwykłego wielokąta to odległość między środkiem a jedną z boków, podczas gdy promień odpowiada odległości między środkiem a wierzchołkiem lub narożnikiem rysunku.

Kryteria zgodności są często stosowane, ponieważ wiele części i wszystkich rodzajów jest produkowanych w szeregu i muszą mieć tę samą formę i środki. W ten sposób można je łatwo wymienić w razie potrzeby, na przykład nakrętki, śruby, arkusze lub bruku ziemi na ulicy.

Może ci służyć: zasada Simpsona: formuła, demonstracja, przykłady, ćwiczeniaRysunek 2. Street Bloblestones to przystające postacie, ponieważ ich kształt i wymiary są dokładnie takie same, chociaż ich orientacja na podłodze może się zmienić. Źródło: Pixabay.

Zgodność, tożsamość i podobieństwo

Na przykład istnieją pojęcia geometryczne związane z zgodnością Identyczne postacie i Podobne liczby, które niekoniecznie oznaczają, że liczby są zgodne.

Należy zauważyć, że przystające liczby są identyczne, jednak czworobok na rycinie 1 może być zorientowany na różne sposoby na samolocie i nadal są zgodne, ponieważ inna orientacja nie zmienia wielkości ich boków lub ich kątów. W takim przypadku przestaliby być identyczny.

Inną koncepcją jest podobieństwo liczb: dwie płaskie liczby są podobne, jeśli mają tę samą formę, a ich wewnętrzne kąty mierzą to samo, chociaż rozmiar liczb może być inny. Jeśli tak jest, liczby nie są zgodne.

Przykłady zgodności

- Zgodność kątów

Jak wskazaliśmy na początku, przystające kąty mają tę samą miarę. Istnieje kilka sposobów na uzyskanie przystających kątów:

Przykład 1

Dwie linie o wspólnym punkcie definiują dwa kąty, zwane Przeciwne kąty przez wierzchołek. Kąty te mają tę samą miarę, dlatego są przystające.

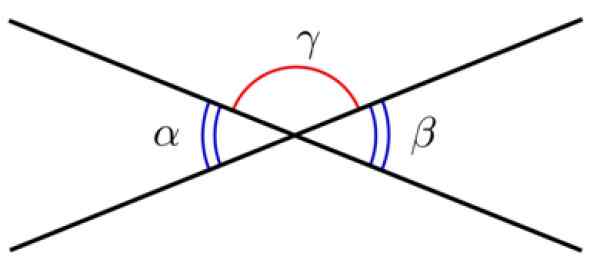Rysunek 3. Przeciwne kąty przez wierzchołek. Źródło: Wikimedia Commons.

Przykład 2

Istnieją dwie równoległe linie plus linia T który ich przecina oboje. Jak w poprzednim przykładzie, gdy ta linia przecina podobieństwa, generuje przystające kąty, jeden po każdej linii po prawej stronie i dwa inne po lewej stronie. Rysunek pokazuje α i α1, na prawo od linii T, Są przystające.

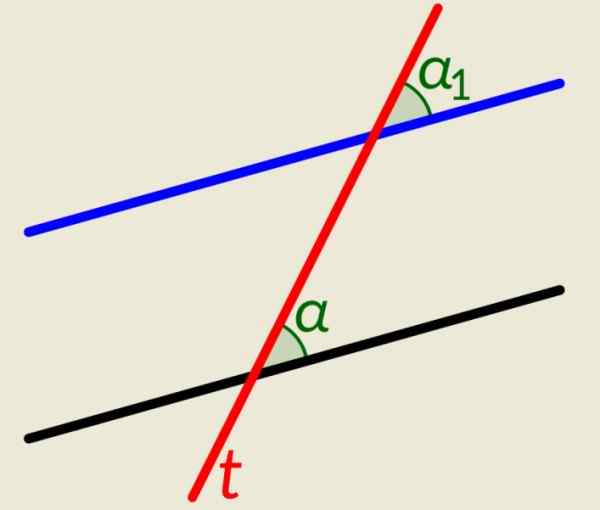Rysunek 4. Kąty pokazane na rysunku są zgodne. Źródło: Wikimedia Commons. Lfahlberg/cc by-sa (https: // creativeCommons.Org/licencje/by-sa/3.0).

Przykład 3

W równoległoboku istnieją cztery wewnętrzne kąty, które są przystające od dwóch do dwóch. Są to między przeciwnymi wierzchołkami, jak pokazano na poniższym rysunku, na którym dwa zielone kąty są zgodne, a także dwa kąty na czerwono.

Może ci służyć: trójkąt acutangle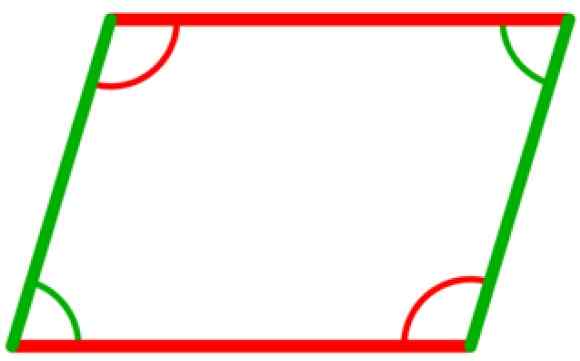Rysunek 5. Wewnętrzne kąty równoległoboku są przystające od dwóch do dwóch. Źródło: Wikimedia Commons.

- Zgodność trójkątów

Dwa trójkąty o identycznych kształtach i tej samej wielkości są przystające. Aby to sprawdzić, istnieją trzy kryteria, które można zbadać w poszukiwaniu zgodności:

-Kryteria LLL: Trzy strony trójkątów mają takie same miary, dlatego L1 = L '1; L2 = L '2 i ja3 = L '3.

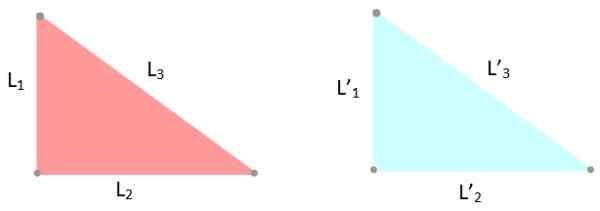Rysunek 6. Przykład przystających trójkątów, których strony mierzą to samo. Źródło: f. Zapata.

-Kryteria alla y aal: Trójkąty mają dwa równe kąty wewnętrzne, a strona między tymi kątami ma tę samą miarę.

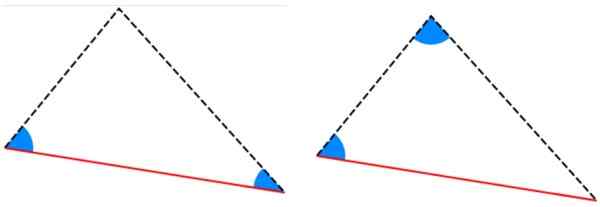Rysunek 7. Kryteria Ala i AAL za zgodność trójkątów. Źródło: Wikimedia Commons.

-Kryteria LAL: Dwie boki są identyczne (odpowiadające), a wśród nich jest ten sam kąt.

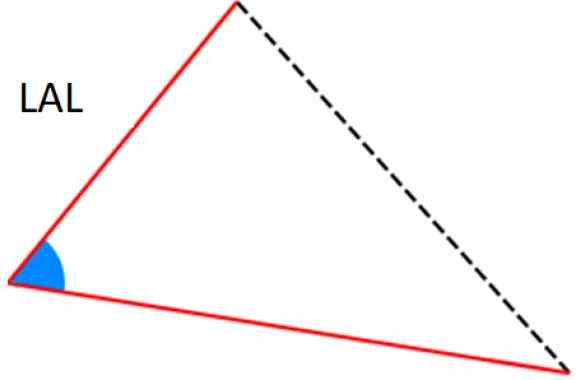Cyfra 8. LAL Kryteria zgodności trójkątów. Źródło: Wikimedia Commons.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Na poniższym rysunku pokazano dwa trójkąty: δABC i δecf. Wiadomo, że AC = EF, że AB = 6 i że CF = 10. Ponadto kąty ∡bac i ∡fec są przystające, a kąty ∡acb i ∡fcb są również.

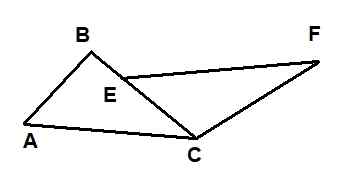Rysunek 9. Trójkąty w przykładzie rozwiązane 1. Źródło: f. Zapata.

Wówczas długość segmentu BE jest równa:

(i) 5 

(Ii) 3

(Iii) 4 

(Iv) 2

(v) 6

Rozwiązanie

Ponieważ dwa trójkąty mają jedną stronę równej długości AC = EF między równymi kątami ∡bac = ∡cef i ∡bca = ∡cfe, można powiedzieć, że dwa trójkąty są zgodne z kryteriami skrzydła.

To znaczy δbac ≡ δcef, więc musisz:

BA = CE = AB = 6

BC = CF = 10

AC = EF

Ale segment, który chcesz obliczyć, jest = BC - EC = 10 - 6 = 4.

Tak, że poprawna odpowiedź to (iii).

- Ćwiczenie 2

Na rysunku pokazano trzy trójkąty. Wiadomo również, że dwa wskazane kąty mierzą 80º i że segmenty AB = PD i AP = CD. Znajdź wartość kąta X wskazaną na rysunku.

Może ci służyć: grafika polibal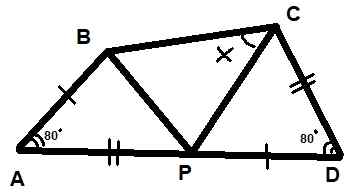Rysunek 10. Trójkąty w przykładzie rozwiązane 2. Źródło: f. Zapata.

Rozwiązanie

Musisz zastosować właściwości trójkątów, które są szczegółowe krok po kroku.

Krok 1

Począwszy od kryteriów zgodności trójkątów Lal, można powiedzieć, że trójkąty BAP i PDC są zgodne:

ΔBAP ≡ δpdc

Krok 2

Powyższe prowadzi do potwierdzenia, że ​​BP = PC, dlatego trójkąt δBPC to izosceles i ∡pcb = ∡pbc = x.

Krok 3

Jeśli nazwiemy γ pod kątem BPC, następuje:

2x + γ = 180º

Krok 4

A jeśli wywołamy β do kątów APB i DCP i α pod kątem ABP i DPC, musi:

α + β + γ = 180º (ponieważ APB jest płaskim kątem).

Krok 5

Ponadto, α + β + 80º = 180º według suma wewnętrznych kąty trójkąta APB.

Krok 6

Łącząc wszystkie te wyrażenia, które musisz:

α + β = 100º

Krok 7

I dlatego:

γ = 80º.

Krok 8

Wreszcie następuje:

2x + 80º = 180º

Z x = 50º.

Bibliografia

  1. Baldor, a. 1973.Płaska i przestrzeń geometria. Cultural American Cultural.
  2. Fundacja CK-12. Zgodne z wielokątami. Źródło: CK 12.org.
  3. Ciesz się matematyką. Definicje: Radio (Polygon). Odzyskane z: FaveMatimaticas.com.
  4. Odniesienie do otwartego matematyki. Testowanie wielokątów pod kątem zgodności. Odzyskane z: Mathpenref.com.
  5. Wikipedia. Zgodność (geometria). Odzyskane z: jest.Wikipedia.org.
  6. Zapata, f. Trójkąty, historia, elementy, klasyfikacja, właściwości. Pobrano z: Lifer.com.