Jak uzyskać kąt trójkąta? (Przykład)

Istnieją różne sposoby Oblicz boki i kąty trójkąta. Zależą one od rodzaju trójkąta, z którym pracujesz.

Przy tej okazji pokazano, jak obliczyć boki i kąty prawego trójkąta, zakładając, że niektóre dane trójkąta z znajomymi z znajomością.

Elementy, które będą używane, to:

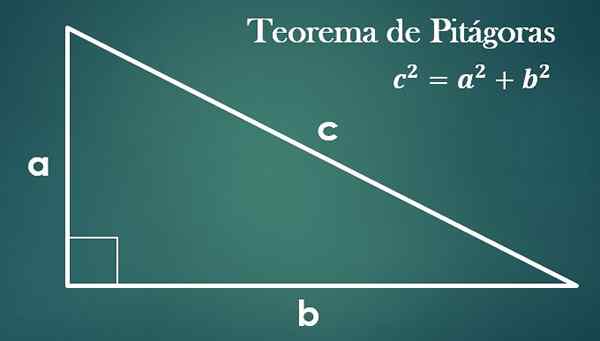
- twierdzenie Pitagorasa

Biorąc pod uwagę trójkąt prostokąta z „A”, „B” i hipotenusą „C”, prawdą jest, że „C² = A²+B²”.

- Obszar trójkąta

Formuła obliczania obszaru dowolnego trójkąta to a = (b × h)/2, gdzie „b” jest długością podstawy i „h” długości wysokości.

- Kąty trójkąta

Suma trzech wewnętrznych kątów trójkąta wynosi 180 °.

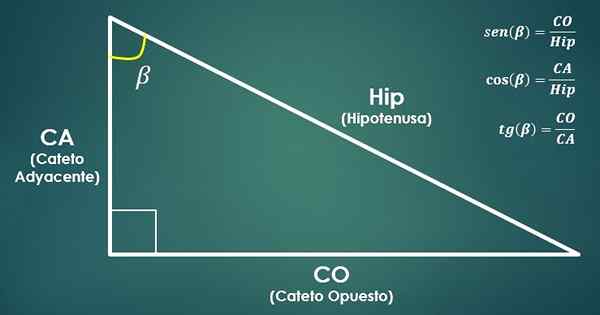
- Funkcje trygonometryczne:

Rozważ odpowiedni trójkąt. Następnie funkcje trygonometryczne są zdefiniowane zatoki, cosinus i styczna kąta beta (β) w następujący sposób:

sin (β) = co/hyp, cos (β) = ca/biodro i tan (β) = co/ca.

Jak obliczyć boki i kąty prawego trójkąta?

Biorąc pod uwagę trójkąt prostokąta ABC, można przedstawić następujące sytuacje:

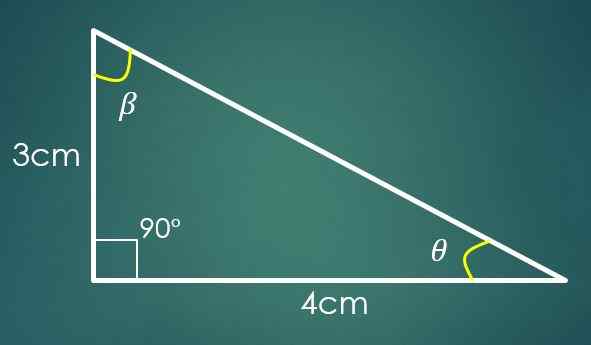
1- Dwie nogi są znane

Jeśli Cateto „A” mierzy 3 cm, a Cateto „B” mierzy 4 cm, aby obliczyć wartość „C”, zastosowane jest twierdzenie Pitagorasa. Zastępując wartości „A” i „B”, uzyskuje się, że C² = 25 cm², co oznacza, że ​​C = 5 cm.

Teraz, jeśli kąt β jest przeciwny do kategorii „B”, wówczas sin (β) = 4/5. Podczas stosowania odwrotnej funkcji piersi, w tej ostatniej równości uzyskuje się, że β = 53,13º. Znane są już dwa wewnętrzne kąty trójkąta.

Niech θ będzie kątem, który pozostaje znany, a następnie 90º+53,13º+θ = 180 °, gdzie uzyskuje się, że θ = 36,87º.

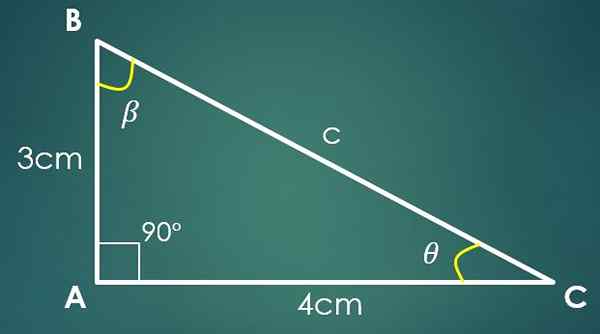
W takim przypadku nie jest konieczne, aby znane strony były dwiema nogami, ważne jest, aby znać wartość dowolnych dwóch stron.

2- noga i obszar jest znany

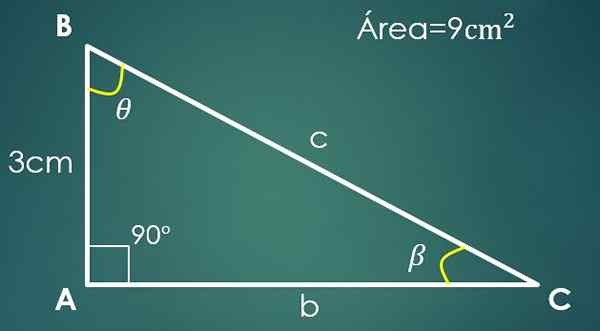
Niech a = 3 cm znanej nogi i 9 cm² obszar trójkąta.

W trójkącie prostokąta kategoria można uznać za podstawę, a drugą jako wysokość (ponieważ są one prostopadłe).

Załóżmy, że „a” jest zatem podstawą 9 = (3 × h)/2, gdzie uzyskuje się, że inna kategoria mierzy 6 cm. Aby obliczyć hipotencję, kontynuuj jak w poprzednim przypadku i uzyskuje się, że c = √45 cm.

Teraz, jeśli kąt β jest przeciwny do „a” cateto, to sin (β) = 3/√45. Podczas usuwania β uzyskuje się, że jego wartość wynosi 26,57º. Wystarczy znać wartość trzeciego kąta θ.

Jest spełnione, że 90 °+26,57º+θ = 180 °, gdzie stwierdzono, że θ = 63,43º.

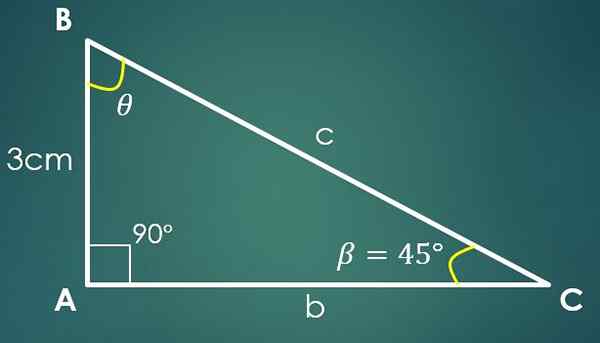
3- Kąt i cateto jest znane

Niech β = 45 ° znany kąt i a = 3 cm znanej nogi, w której cateto „a” jest przeciwny kątowi β. Za pomocą formuły stycznej uzyskuje się, że TG (45 °) = 3/Ca, gdzie okazuje się, że Ca = 3 cm.

Za pomocą twierdzenia Pitagorasa uzyskuje się, że c² = 18 cm², to znaczy C = 3√2 cm.

Wiadomo, że kąt mierzy 90 ° i że β mierzy 45 °, stąd stwierdzono, że trzeci kąt mierzy 45 °.

W tym przypadku znaną stroną nie musi być nogą, może to być żadna z trzech stron trójkąta.