Obciążenie osiowe Jak obliczone i rozwiązane ćwiczenia

Obciążenie osiowe Jest to siła kierowana równolegle do osi symetrii elementu, który tworzy strukturę. Siła osiowa lub obciążenie może być napięciem lub kompresją. Jeśli linia działania siły osiowej pokrywa się z osą symetrii, która przechodzi przez środowisko rozważanego elementu, mówi się, że jest to koncentryczne obciążenie osiowe lub siłę.

Przeciwnie, jeśli jest to siła osiowa lub obciążenie równolegle do osi symetrii, ale której linia działania nie znajduje się na samej osi, jest to mimośrodowa siła osiowa.

Rysunek 1. Obciążenie osiowe. Źródło: Self Made

Na rycinie 1 żółte strzałki reprezentują siły lub obciążenia osiowe. W jednym przypadku jest to koncentryczna siła napięcia, a w drugiej stawiamy czoła mimośrodowej sile ściskającej.

Jednostka miary obciążenia osiowego w systemie międzynarodowym, jeśli jest to Newton (N). Ale często stosuje się inne jednostki siły, takie jak siła kilograma (kg-f) i siła funta (LB-F) (LB-F).

[TOC]

Jak to jest obliczane?

Aby obliczyć wartość obciążenia osiowego w elementach struktury, należy wykonać następujące kroki:

- Wykonaj schemat siły na każdym elemencie.

- Zastosuj równania, które gwarantują równowagę translacyjną, to znaczy, że suma wszystkich sił jest nieważna.

- Rozważ równanie momentów lub momentów, aby równowaga obrotowa była wypełniona. W tym przypadku suma wszystkich momentów musi być zerowa.

- Oblicz siły, a także zidentyfikuj siły osiowe lub obciążenia w każdym z elementów.

Związek obciążenia osiowego z normalnym wysiłkiem

Średni normalny wysiłek jest definiowany jako iloraz między obciążeniem osiowym podzielonym między przekrój obszaru. Jednostki normalnego wysiłku w systemie międzynarodowym.Siema. Są Newton na metrze kwadratowym (N/ M²) lub Pascal (PA). Ryc. 2 ilustruje koncepcję normalnego wysiłku dla jasności.

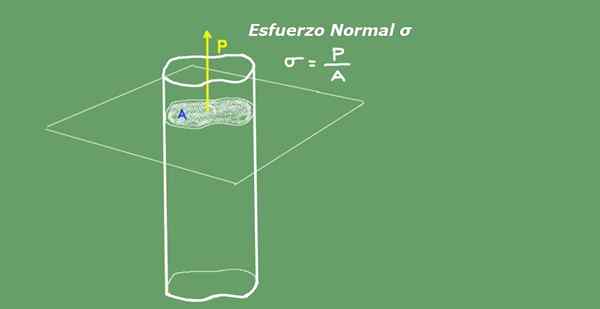Rysunek 2. Normalny wysiłek. Źródło: Self Made.

Rozwiązane ćwiczenia

-Ćwiczenie 1

Rozważ cylindryczną betonową kolumnę H i Radio R. Załóżmy, że gęstość betonu wynosi ρ. Kolumna nie obsługuje żadnego dodatkowego obciążenia niż własna waga i jest wspierana na prostokątnej podstawie.

- Znajdź wartość obciążenia osiowego w punktach a, b, c i d, które są w następujących pozycjach: a u podstawy kolumny, b a ⅓ wysokości h, c a ⅔ wysokości H i ostatnie d na górnym końcu kolumny.

- Określ także średni normalny wysiłek w każdej z tych pozycji. Weź następujące wartości numeryczne: h = 3m, r = 20 cm i ρ = ​​2250 kg/m3

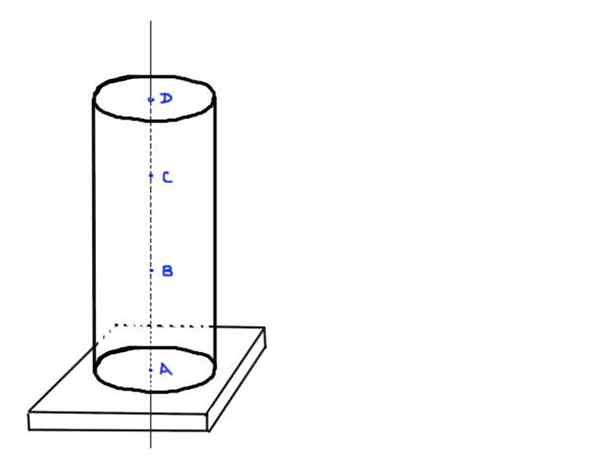Rysunek 3. Cylindryczna kolumna. Źródło: Self Made.

Rozwiązanie

Całkowita waga kolumny

Całkowita waga W kolumny jest iloczynem jej gęstości przez objętość pomnożoną przez przyspieszenie grawitacji:

W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 n

Obciążenie osiowe w

W punkcie do kolumny musi podtrzymywać całą wagę, aby obciążenie osiowe w tym punkcie kompresja jest równa wagi kolumny:

PA = w = 8313 n

Obciążenie osiowe w B

Na punkcie B będzie sam ⅔ kolumny, więc obciążenie osiowe w tym punkcie będzie kompresja, a jego wartość masy kolumny:

Pb = ⅔ w = 5542 n

Rysunek 3. Cylindryczna kolumna. Źródło: Self Made.

Powyżej pozycji C jest tylko kolumna ⅓, więc jej obciążenie kompresyjne osiowe będzie ⅓ własnej wagi:

PC = ⅓ w = 2771 n

Obciążenie osiowe w D

Wreszcie w punkcie D, czyli górnym końcu kolumny, nie ma obciążenia, więc siła osiowa w tym punkcie jest nieważna.

PD = 0 N

Normalne wysiłki na każdej z pozycji

Aby określić normalny wysiłek w każdej z pozycji, konieczne będzie obliczenie przekroju obszaru A, który jest podany przez:

A = π ∙ R² = 0,126m²

W ten sposób normalny wysiłek w każdej z pozycji będzie iloraz między siłą osiową w każdym z punktów podzielonych między przekrój już obliczonym, co w tym ćwiczeniu jest takie same dla wszystkich punktów, ponieważ jest to kolumna cylindryczna.

σ = p/a; σa = 66,15 kPa; σB = 44,10 kPa; σc = 22,05 kPa; σd = 0,00 kPa

-Ćwiczenie 2

Rysunek pokazuje strukturę złożoną z dwóch pasków, które nazwiemy AB i CB. Pasek AB jest wspierany na końcu A One przez szpilkę, a na drugim końcu podłączonym do drugiego paska za pośrednictwem drugiego B -pin.

Podobnie pasek CB jest obsługiwany na końcu C za pomocą szpilki, a na końcu B z pinem B, który łączy go do drugiego paska. Siła pionowa lub obciążenie F jest nakładana do pinów B, jak pokazano na poniższym rysunku:

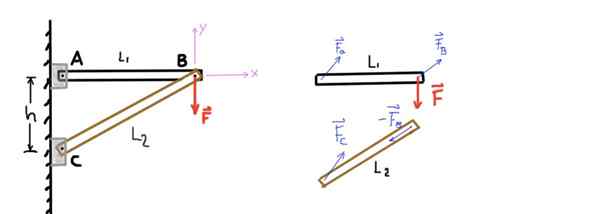Rysunek 4. Dwie bary struktura i bezpłatny schemat ciała. Źródło: Self Made.

Załóż, że waga słupków jest nikczemna, ponieważ siła f = 500 kg-f jest znacznie większa niż waga konstrukcji. Oddzielenie między podparciem a i c wynosi h = 1,5 m, a długość paska AB wynosi l1 = 2 m. Określ obciążenie osiowe w każdym z słupków, wskazując, czy jest to kompresja osiowa, czy obciążenie napięcia.

Rozwiązanie 2

Rysunek pokazuje, poprzez schemat wolnego ciała, siły działające na każdy elementy struktury. Wskazany jest również kartezjański układ współrzędnych.

Dorady lub momenty zostaną obliczone w punkcie B i będą uważane za pozytywne, jeśli wskazują na ekran (oś z). Równowaga sił i momentów dla każdego paska to:

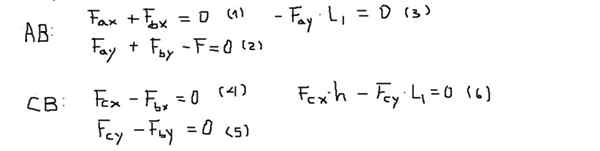
Następnie elementy sił każdego z równań są jasne po następującej kolejności:

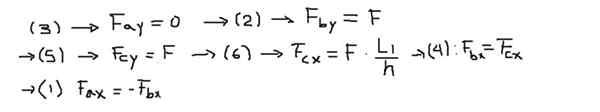
Wreszcie, powstałe siły są obliczane na końcach każdego paska:

Można zauważyć, że siły na końcach każdego z słupków są do nich równoległe, potwierdzając, że są to siły osiowe lub obciążenia. W przypadku paska AB jest to siła napięcia osiowego, której wartość to:

F ∙ (L1/H) = 500 kg-f ∙ (2,0 m/1,5 m) = 666,6 kg-f = 6533,3 n

Pasek CB jest w kompresji z powodu dwóch sił, które działają na ich końcach, które są równoległe do paska i wskazują na ich centrum. Wielkość siły ściskającej osiowej w pasku CB wynosi:

F ∙ (1 + l1²/h²) 1/2 = 500 kg-f ∙ (1 + (2/1,5) ²) 1/2 = 833,3 kg-f = 8166,6 n

Bibliografia

1. Piwo F ... mechanika materiałowa. 5. Wydanie. 2010. MC Graw Hill. 1-130.
2. Hibbeler R. Mechanika materiałów. Ósme wydanie. Prentice Hall. 2011. 3-60.
3. Gere J. Mechanika materiałów. Ósme wydanie. Cengage Learning. 4-220.
4. Giancoli, zm. 2006. Fizyka: zasady z aplikacjami. 6. edycja. Prentice Hall. 238-242.
5. Valera Negrete, J. 2005. Ogólne uwagi fizyki. Unam. 87-98.